题目内容
15．假如认为月球绕地球是做匀速圆周运动，以下说法中正确的是（ ）| A． | 月球受到地球的引力是不变的 | |
| B． | 除了受到地球的引力外，月球还受到其他星球的引力，所有这些引力的合力等于零 | |
| C． | 月球所受到各种引力之合力的大小有变化 | |
| D． | 月球受到各种引力的合力大小不变，方向在不断改变 |
分析 绕地球做匀速圆周运动的月球，万有引力和月球受到的其他的作用力的合力提供向心力．月球做匀速圆周运动的向心力大小不变，方向时刻改变．
解答 解：A、力是矢量，月球受到地球的引力的方向始终指向地球的球心，方向不断变化．故A错误；
B、C、D、由于月球做匀速圆周运动，所以受到的合外力始终指向地球的球心，方向是不断变化．
所以若月球还受到其他星球的引力，所有这些引力的合力与地球对月球的引力的和提供向心力，所以这些力的和也是指向地球的球心，大小保持不变．故BC错误，D正确．
故选：D
点评 本题考查万有引力的应用，应明确所有天体的圆周运动都是因为受到了万有引力的作用．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
甲、乙两列简谐横波在同一介质中分别沿x轴正向和负向传播，波速均为25cm/s，两列波在t=0时的波形曲线如图所示．两列波发生叠加．
关于验证平行四边形定则的实验，请回答下列问题：
10．
绕有线圈的铁芯直立在水平桌面上，铁芯上套着一个铝环，线圈与电源、电键相连，如图所示．线圈上端与电源正极相连，闭合电键的瞬间，铝环向上跳起．若保持电键闭合，则（ ）
绕有线圈的铁芯直立在水平桌面上，铁芯上套着一个铝环，线圈与电源、电键相连，如图所示．线圈上端与电源正极相连，闭合电键的瞬间，铝环向上跳起．若保持电键闭合，则（ ）| A． | 铝环不断升高 | |
| B． | 铝环停留在某一高度 | |
| C． | 铝环跳起到某一高度后将回落 | |
| D． | 如果电源的正、负极对调，重做实验铝环不会向上跳 |
20．
如图所示，一绝缘轻杆长为d，中心固定在转轴O上，左侧挂有一定质量的矩形闭合金属框，下边边长为L，并放在匀强磁场中，当在线框中通电流I后，在最右端挂一质量为m的重物，轻杆恰能平衡；若电流方向不变，大小变为2I，则m挂在距O点$\frac{1}{6}$d，恰又能平衡，则以下说法正确的是（ ）
如图所示，一绝缘轻杆长为d，中心固定在转轴O上，左侧挂有一定质量的矩形闭合金属框，下边边长为L，并放在匀强磁场中，当在线框中通电流I后，在最右端挂一质量为m的重物，轻杆恰能平衡；若电流方向不变，大小变为2I，则m挂在距O点$\frac{1}{6}$d，恰又能平衡，则以下说法正确的是（ ）| A． | 金属框的质量可能为$\frac{5}{3}$m | |
| B． | 匀强磁场的磁感应强度大小可能为$\frac{2mg}{3IL}$ | |
| C． | 金属框的质量可能为$\frac{8}{3}$m | |
| D． | 匀强磁场的磁感应强度大小可能为$\frac{4mg}{3IL}$ |
7．下述做法能改善空气质量的是（ ）
| A． | 以煤等燃料作为主要生活燃料 | |
| B． | 利用太阳能、风能和氢能等能源替代化石能源 | |
| C． | 鼓励私人购买和使用汽车代替公交车 | |
| D． | 限制使用电动车 |
4．
如图所示，某同学用DIS设计了一个测物体瞬时速度的实验．
第一次实验时，该同学在小车上固定挡光片时，使挡光片的前端朝向车头．依次更换四个挡光片，将小车从轨道上同一位置P由静止释放，获得了4组实验数据．第二次实验时，他将挡光片倒置，使挡光片的前端朝向车尾，仍将小车从轨道上同一位置P由静止释放，又得到了4组实验数据．实验完毕，得到两张表格．
表一
表二
分析表格中的数据，可知表一是将挡光片倒置后所得数据；四个挡光片中，最窄的挡光片的宽度△s=0.020m（结果保留到小数点后第三位）；表中与小车车头到达光电门时的瞬时速度最接近的是0.342m/s．
如图所示，某同学用DIS设计了一个测物体瞬时速度的实验．第一次实验时，该同学在小车上固定挡光片时，使挡光片的前端朝向车头．依次更换四个挡光片，将小车从轨道上同一位置P由静止释放，获得了4组实验数据．第二次实验时，他将挡光片倒置，使挡光片的前端朝向车尾，仍将小车从轨道上同一位置P由静止释放，又得到了4组实验数据．实验完毕，得到两张表格．
表一
| 不同的挡光片 | 通过光电门的时间（s） | 速度（m/s） |
| A | 0.15425 | 0.519 |
| B | 0.11209 | 0.535 |
| C | 0.07255 | 0.551 |
| D | 0.03510 | 0.570 |
| 不同的挡光片 | 通过光电门的时间（s） | 速度（m/s） |
| A | 0.23048 | 0.349 |
| B | 0.17454 | 0.345 |
| C | 0.11562 | 0.344 |
| D | 0.05860 | 0.342 |
7．
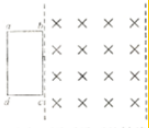如图所示，空间存在宽度为3L、磁感应强度大小为B、方向垂直纸面向里的有界匀强磁场．均匀导线绕制的单匝矩形线框abcd，在纸面内从静止开始做加速度为a0的匀加速直线运动，速度方向垂直磁场边界向右．开始时，bc边紧挨着磁场左边界，运动中bc边与磁场边界平行．线框边长ab=L，bc=2L，其总电阻为R，则线框从进入到穿出磁场的过程中，下列说法正确的是（ ）
如图所示，空间存在宽度为3L、磁感应强度大小为B、方向垂直纸面向里的有界匀强磁场．均匀导线绕制的单匝矩形线框abcd，在纸面内从静止开始做加速度为a0的匀加速直线运动，速度方向垂直磁场边界向右．开始时，bc边紧挨着磁场左边界，运动中bc边与磁场边界平行．线框边长ab=L，bc=2L，其总电阻为R，则线框从进入到穿出磁场的过程中，下列说法正确的是（ ）| A． | 流过线框截面的总电量为$\frac{4B{L}^{2}}{R}$ | |
| B． | 线框回路中始终有顺时针方向的感应电流 | |
| C． | ad边进入磁场前瞬间bc间的电势差为$\frac{2BL\sqrt{2{a}_{0}L}}{3}$ | |
| D． | ad边离开磁场前瞬间bc间的电势差为$\frac{4BL\sqrt{2{a}_{0}L}}{3}$ |