��Ŀ����
����Ŀ����ͼ���뾶 R=0.8m ���ķ�֮һԲ���ι⻬�����ֱ���ã�Բ����͵� D�볤ΪL��ˮƽ��������D�㣬����M=1.0kg��С����A��Բ������C�ɾ�ֹ�ͷţ�������͵�D�����D��m=0.5kg�ľ�ֹС��� B����������A���ٶȱ�ΪvA=2.0m/s���������˶�����֪�������ˮƽ���Ķ�Ħ��������Ϊ=0.1��A��B ������Ϊ�ʵ㣬B��E������ֱ��������ʱû�л�е����ʧ��ȡg=10m/s2.��
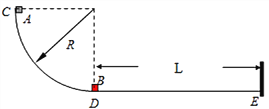
(1)����A�յ���Բ������͵�Dʱ��Բ����ѹ����
(2)���� B ������˲����ٶȣ�
(3)Ҫʹ�������ܷ����ڶ�����ײ��DE�ij��� L Ӧ�����������
���𰸡���1��F��30 N��2��vB��4 m/s��3��L��5m
�������������������1����С�����˶���D����ٶ�Ϊv���ɻ�е���غ㶨���У�MgR��![]() Mv2(2��)
Mv2(2��)
��D�㣬��ţ�ٵڶ������У�F - Mg��M![]() (2��)
(2��)
�����ã� F��30 N (1��)
��ţ�ٵ������ɣ�С������D��ʱ��Բ����ѹ��Ϊ30N (1��)
(2) ��B���鱻������ٶ�ΪvB���ɶ����غ㶨�ɣ�M v��MvA+mvB (3��)
�ã� vB��4 m/s ��1�֣�
(3) ����B�����ٶȽϴ�����������ٴ�����һ��������B����ֱ���嵯�غ�����������˶������ֹͣ���ﵽ����·�̣���
����A��飬�ɶ��ܶ�����![]() (2��)
(2��)
��ã�SA="2" m ��1�֣�
����B��飬����B����ֱ�������ײ��е����ʧ���ɶ��ܶ�����
![]() (2��)
(2��)
��ã�SB="8" m��1�֣�
������պõڶ��η����Ӵ�������2L=SA+ SB="10" m ��1�֣�
Ҫʹ�������ܷ����ڶ�����ײL��5m ��1�֣�