题目内容
14.如图甲所示,相距为L=1m的光滑足够长平行金属导轨水平放置,导轨一部分处在垂直于导轨平面的匀强磁场中,OO′为磁场边界,磁感应强度为B=0.4T,导轨右侧接有定值电阻R=10?,导轨电阻忽略不计.在距OO′为L处垂直导轨放置一质量为m=0.5㎏、电阻不计的金属杆ab.若ab杆在恒力作用下由静止开始向右运动3L的距离,其v-s的关系图象如图乙所示,其中v1=2m/s,v2=6m/s,求:
(1)在金属杆ab穿过磁场的过程中,通过ab杆的感应电流方向;
(2)金属杆ab离开磁场后的加速度a;
(3)金属杆ab在离开磁场前瞬间的加速度a′;
(4)在整个过程中电阻R上产生的电热Q1是多少?
分析 (1)根据右手定则判断感应电流方向.
(2)由匀变速直线运动的速度位移公式可以求出加速度.
(3)根据法拉第定律、欧姆定律、安培力和牛顿第二定律结合求加速度.
(4)根据法拉第电磁感应定律求出线框中感应电动势.根据焦耳定律和正弦交变电流的特点求出电阻R上产生的焦耳热Ql.
解答 解:(1)由右手定则可知,杆中电流方向为由b到a.
(2)金属杆离开磁场后做匀加速直线运动,
由速度位移公式得,加速度:a=$\frac{{v}_{2}^{2}-{v}_{1}^{2}}{2(3L-L)}$=$\frac{{v}_{2}^{2}-{v}_{1}^{2}}{4L}$=$\frac{36-4}{4×1}$=8m/s2;
(3)ab杆在离开磁场前瞬间,水平方向上受安培力F安和外力F作用,设加速度为a′,
安培力:F安=BIL,感应电流:I=$\frac{BL{v}_{1}}{R}$,
由牛顿第二定律得:a′=$\frac{F-{F}_{安}}{m}$,
解得:a′=$\frac{{v}_{2}^{2}-{v}_{1}^{2}}{4L}$-$\frac{{B}^{2}{L}^{2}{v}_{1}}{mR}$=8-$\frac{0.16×1×2}{0.5×10}$=1.6m/s2;
(4)ab杆在位移L到3L的过程中,由动能定理得:F(3L-L)=$\frac{1}{2}$(v22-v12)
ab杆在磁场中发生L位移过程中,恒力F做的功等于ab杆增加的动能和回路产生的电
能(即电阻R上产生的电热Q1),由能量守恒定律得:FL=$\frac{1}{2}$mv12+Q1 ,
解得:Q1=$\frac{m({v}_{2}^{2}-{v}_{1}^{2})}{4}$=$\frac{0.5×(36-4)}{4}$=4J;
答:(1)在金属杆ab穿过磁场的过程中,通过ab杆的感应电流方向:由b到a;
(2)金属杆ab离开磁场后的加速度a为8m/s2;
(3)金属杆ab在离开磁场前瞬间的加速度a′为1.6m/s2;
(4)在整个过程中电阻R上产生的电热Q1是4J
点评 要能够把法拉第电磁感应定律与电路知识结合运用.电磁感应中动力学问题离不开受力分析和运动过程分析.关于电磁感应中能量问题我们要从功能关系角度出发研究.

| A. | 开普勒进行了“月-地检验”,说明天上和地下的物体都遵从万有引力定律 | |
| B. | 伽利略不畏权威,通过“理想斜面实验”,科学地推理出“力不是维持物体运动的原因” | |
| C. | 哥白尼提出日心说并发现了太阳系中行星沿椭圆轨道运动的规律 | |
| D. | 奥斯特发现了电磁感应现象,使人类从蒸汽机时代步入了电气化时代 |
 如图所示,水下点光源S向水面A点发射一束复色光线,折射后光线分成a,b两束,则下列说法不正确的是( )
如图所示,水下点光源S向水面A点发射一束复色光线,折射后光线分成a,b两束,则下列说法不正确的是( )| A. | 在水中a光的速度比b光的速度小 | |
| B. | 通过同一个单缝发生衍射时,b光中央明条纹比a光中央明条纹宽 | |
| C. | 若a、b两种单色光由水中射向空气发生全反射时,a光的临界角较小 | |
| D. | 用同一双缝干涉实验装置做实验,a光的相邻干涉条纹间距大于b光的相邻干涉条纹间距 |
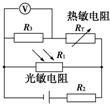 如图所示RT为正温度系数热敏电阻,R1为光敏电阻,R2和R3均为定值电阻,电源电动势为E,内阻为r,V为理想电压表,现发现电压表示数增大,可能的原因是( )
如图所示RT为正温度系数热敏电阻,R1为光敏电阻,R2和R3均为定值电阻,电源电动势为E,内阻为r,V为理想电压表,现发现电压表示数增大,可能的原因是( )①热敏电阻温度升高,其他条件不变
②热敏电阻温度降低,其他条件不变
③光照增强,其他条件不变
④光照减弱,其他条件不变.
| A. | ①③ | B. | ①④ | C. | ②③ | D. | ②④ |
| A. | 12m/s | B. | 14m/s | C. | 18m/s | D. | 24m/s |
 t=0时刻位于坐标原点O的波源沿y轴方向开始振动,形成沿x轴正方向传播的简谐横波,t=5s时波源停止振动,t=6.5s时的波形图如图所示,此刻质点P的平衡位置与O点的距离x=4m.下列说法正确的是( )
t=0时刻位于坐标原点O的波源沿y轴方向开始振动,形成沿x轴正方向传播的简谐横波,t=5s时波源停止振动,t=6.5s时的波形图如图所示,此刻质点P的平衡位置与O点的距离x=4m.下列说法正确的是( )| A. | 0~4s时间内质点P运动的总路程为80m | |
| B. | t=0时刻波源的振动方向沿y轴负方向 | |
| C. | t=7s时刻质点P位于波峰 | |
| D. | t=6.5s时刻开始质点Q比质点P第一次先回到平衡位置 |
 如图所示,两根等长的绳子AB和BC吊一重物静止,两根绳子与水平方向夹角均为60°.现保持绳子AB与水平方向的夹角不变,而将绳子BC逐渐缓慢地变化到沿水平方向,在这一过程中,绳子BC的拉力变化情况是( )
如图所示,两根等长的绳子AB和BC吊一重物静止,两根绳子与水平方向夹角均为60°.现保持绳子AB与水平方向的夹角不变,而将绳子BC逐渐缓慢地变化到沿水平方向,在这一过程中,绳子BC的拉力变化情况是( )| A. | 逐渐增大 | B. | 先逐渐减小,后逐渐增大 | ||
| C. | 逐渐减小 | D. | 先逐渐增大,后逐渐减小 |
 如图,质量为M的导热性能极好的气缸,高为L,开口向上置于水平地面上,气缸中有横截面积为S、质量为m的光滑活塞,活塞将一定质量的理想气体封闭在气缸内.外界温度为t1、大气压为p0,此时气柱高度为l,气缸和活塞的厚度均可忽略不计,重力加速度为g.
如图,质量为M的导热性能极好的气缸,高为L,开口向上置于水平地面上,气缸中有横截面积为S、质量为m的光滑活塞,活塞将一定质量的理想气体封闭在气缸内.外界温度为t1、大气压为p0,此时气柱高度为l,气缸和活塞的厚度均可忽略不计,重力加速度为g.