��Ŀ����
����Ŀ����ͼ��ʾ��ֱ�������еĵ�һ�����д�����y�Ḻ�������ǿ�糡���ڵڶ������д��ڴ�ֱֽ���������ǿ�ų���һ�����Ϊq������Ϊm�Ĵ���������ӣ��ڨCx���ϵ�a�����ٶ�v0��Cx���60��Ƚ�����ų�����y = L����b�㴹ֱ��y�᷽�����糡��������x����x=2L����c�㡣������������

(1)�Ÿ�Ӧǿ��B�Ĵ�С��
(2)�糡ǿ��E�Ĵ�С��
(3)�����ڴų��͵糡�е��˶�ʱ��֮�ȡ�
���𰸡�(1) ![]() (2)
(2) ![]() (3)
(3) ![]()
��������������������ɼ���֪ʶ������ӵĹ���뾶��Ȼ����ţ�ٵڶ���������Ÿ�Ӧǿ�ȴ�С�������ڵ糡������ƽ���˶�������ƽ���˶���������糡ǿ�ȴ�С����������ڴų��е��˶�ʱ�����ڵ糡�е��˶�ʱ�䣬Ȼ�����ʱ��֮�ȣ�
(1)���ӵ��˶��켣��ͼ��ʾ��
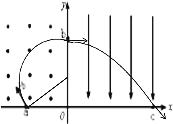
�ɼ���֪ʶ�ɵã�r+rsin30��=L
�����ڴų�����Բ���˶��Ĺ���뾶�� ![]()
�����ڴų���������Բ���˶������������ṩ��������
��ţ�ٵڶ����ɵã� ![]()
��ã� ![]()
(2)�����ڵ糡������ƽ���˶���
ˮƽ����2L=v0t
��ֱ���� ![]()
��ã� ![]()
(3)�����ڴų�����Բ���˶������ڣ� ![]()
�ɼ���֪ʶ��֪�������ڴų���ת����Բ�Ľǣ���=180��-60��=120��
�����ڴų�����Բ���˶���ʱ�䣺 ![]()
�����ڵ糡�е��˶�ʱ�䣺 ![]()
�����ڴų��͵糡�е��˶�ʱ��֮�ȣ� 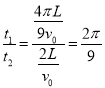

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�












