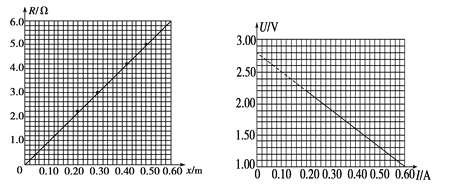
题目内容
【题目】如图所示,在光滑、绝缘的水平面内,有一个正方形MNPQ区域,边长L=1m。半径R=20cm的圆形磁场与MN、MQ边均相切,与MQ边切于点A,磁感应强度B=0.5T,方向垂直于水平面向上。圆形磁场之外区域,有方向水平向左的匀强电场,场强大小E=0.5V/m。两个大小完全相同的金属小球a、b均视为质点。小球a的质量ma=2×10-5kg,电量q=+4×10-4C.小球b的质量mb=1×10-5kg,不带电,放在圆周上的D点静止,A、C、D三点在同一直线上。小球a从A点正对磁场圆心C射入,会与球b在D点沿平行于MN的方向发生弹性碰撞,碰后忽略两球之间的相互作用力及小球重力。π=3.14,求:

(1)小球a射入磁场时的速度大小及小球a射入磁场到与小球b相碰撞经历的时间;
(2)小球a与b碰撞后在正方形MNPQ区域内运动,两球之间的最大距离。
【答案】(1) 2m/s ,0.714s (2) ![]()
【解析】试题分析:由几何关系,可知只有圆周运动的半径r=R时,才能与小球b相撞,从而求得小球a射入磁场时的速度;然后在磁场及电场中用运动学规律,分别求解时间;小球a与b发生弹性碰撞后,分别求出各自碰撞后速度,再用运动学规律求解两球之间的最大距离。
(1)小球a的轨迹如图所示,才能与小球b相撞,故小球a在磁场中做圆周运动的半径r=R
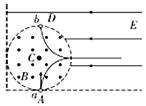
在磁场中![]()
解得:![]()
在磁场中的运动时间![]()
在电场中![]()
![]()
小球a射入磁场到与小球b相碰撞经历的时间![]()
(2)小球a与b发生弹性碰撞有![]()
![]()
解得:![]() ,
,![]()
因两个小球是大小相同的金属球,碰后分开时所带电荷量![]()
因碰后两球的速度均垂直电场方向,故均做类平抛运动。
小球a沿电场方向有![]() ,得a1=5m/s2
,得a1=5m/s2
小球b沿电场方向有![]() ,得a2=10m/s2
,得a2=10m/s2
由于a2>a1,假设小球均未从NP边界穿出,则小球b将先到达MN边界。
小球b沿电场方向的位移![]() ,得tb=0.2s
,得tb=0.2s
此时小球b垂点电场方向的位置为![]()
所以假设成立,如图所示。
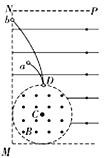
当小球b到达MN边界时刻,小球a与b在正方形MNPQ区域内运动的间距最大。
设最大间距为s,则有![]()
解得:![]()

 应用题作业本系列答案
应用题作业本系列答案