题目内容
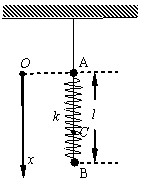
(25分) 如图所示,在一个劲度系数为 k的轻质弹簧两端分别拴着一个质量为 m 的小球A和质量为 2m的小球B.A用细线拴住悬挂起来,系统处于静止状态,此时弹簧长度为![]() .现将细线烧断,并以此时为计时零点,取一相对地面静止的、竖直向下为正方向的坐标轴Ox,原点O与此时A球的位置重合如图.试求任意时刻两球的坐标.
.现将细线烧断,并以此时为计时零点,取一相对地面静止的、竖直向下为正方向的坐标轴Ox,原点O与此时A球的位置重合如图.试求任意时刻两球的坐标.

解法一:
对于由小球A、B和弹簧构成的系统,当A、B之间的距离为l时,已知mA = m,mB = 2m,由质心的定义,可知系统的质心C离A的距离
![]() (1)
(1)
故A、B到质心C的距离分别为
![]() (2)
(2)
若以质心C为参考系(质心系),则质心C是固定不动的,连接A、B的弹簧可以分成两个弹簧CA和CB.设弹簧CA的自然长度为lA0,劲度系数为kA,一端与小球A相连,另一端固定在C点;弹簧CB的的自然长度为lB0,劲度系数为kB,一端与小球B相连,另一端亦固定在C点.若连接A、B的自然长度为l0,根据题意有
![]() (3)
(3)
由(2)式可知弹簧CA和CB的自然长度分别为
![]() (4)
(4)
当A被悬挂,系统处于静止时,已知连接A、B的弹簧长度为l,由(2)式可知,此时弹簧CA和CB的长度分别为
![]() (5)
(5)
弹簧CA、CB作用于A、B的弹簧力分别为
![]()
![]()
但fA 、fB就是连接A、B的弹簧因拉伸而产生的弹力f,即有
![]()
由此得
![]() (6)
(6)
相对地面,质心C是运动的,在t = 0 时刻,即细线刚烧断时刻,A位于Ox轴的原点O处,即![]() ;B的坐标
;B的坐标![]() .由(1)式,可知此时质心C的坐标为
.由(1)式,可知此时质心C的坐标为
![]() (7)
(7)
在细线烧断以后,作用于系统的外力是重力![]() .故质心以g为加速度做匀加速直线运动,任意时刻t,质心的坐标
.故质心以g为加速度做匀加速直线运动,任意时刻t,质心的坐标
![]() (8)
(8)
由于质心作加速运动,质心系是非惯性系.在非惯性参考系中,应用牛顿第二定律研究物体的运动时,物体除受真实力作用外,还受惯性力作用.若在质心系中取一坐标轴![]() ,原点
,原点![]() 与质心C固连,取竖直向下为
与质心C固连,取竖直向下为![]() 轴的正方向,当小球B在这参考系中的坐标为
轴的正方向,当小球B在这参考系中的坐标为![]() 时,弹簧CB作用于B的弹性力
时,弹簧CB作用于B的弹性力
![]()
当![]() 时,方向竖直向上.此外,B还受到重力mg,方向竖直向下;惯性力大小为mg,方向竖直向上.作用于B的合力
时,方向竖直向上.此外,B还受到重力mg,方向竖直向下;惯性力大小为mg,方向竖直向上.作用于B的合力
![]()
由(3)、(4)式得
![]() (9)
(9)
令
![]() (10)
(10)
有
![]() (11)
(11)
当XB = 0,作用于B的合力FB = 0,B处于平衡状态,由(10)式,可知在质心系中,B的平衡位置的坐标
![]() (12)
(12)
XB为B离开其平衡位置的位移,(11)式表明,作用于B的合力具有弹性力的性质,故在FB作用下, B将在平衡位置附近作简谐振动,振动圆频率
![]() (13)
(13)
离开平衡位置的位移
![]() (14)
(14)
AB为振幅,![]() 为初相位.在t = 0时刻,即细线刚烧断时刻,B是静止的,故此时B离开其平衡位置
为初相位.在t = 0时刻,即细线刚烧断时刻,B是静止的,故此时B离开其平衡位置![]() 的距离就是简谐振动的振幅AB,而在t = 0时刻,B离开质心的距离即(5)式给出的lB,故B离开平衡位置的距离即振幅
的距离就是简谐振动的振幅AB,而在t = 0时刻,B离开质心的距离即(5)式给出的lB,故B离开平衡位置的距离即振幅
![]()
由(5)式、(12)式得
![]() (15)
(15)
因t = 0,XB =AB,且XB是正的,故
![]()
由此得
![]() (16)
(16)
由(10)式,t时刻B在质心系中的坐标
![]() (17)
(17)
在地面参考系的坐标
![]() (18)
(18)
得
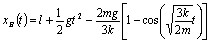 (19)
(19)
同理,当小球A在质心系中的坐标为![]() 时,注意到
时,注意到![]() 是负的,这时,弹簧CA的伸长量为
是负的,这时,弹簧CA的伸长量为
![]() ,
,
当![]() 为负时,弹力向下,为正,当
为负时,弹力向下,为正,当![]() 为正时,弹力向上,为负,故有
为正时,弹力向上,为负,故有
![]()
作用于A的合力为
![]()
令
![]()
有
![]()
当XA=0,作用于A的合力FB = 0,A处于平衡状态,A的平衡位置的坐标
![]() (20)
(20)
XA为A离开其平衡位置的位移,故在合力FA作用下, A将在平衡位置附近作简谐振动,振动圆频率
![]() (21)
(21)
离开平衡位置的位置
![]()
AA为振幅,![]() 为初相位.在t = 0时刻,即细线刚烧断时刻,A是静止的,A离开质心C的距离为lA,A的平衡位置离开质心的距离为
为初相位.在t = 0时刻,即细线刚烧断时刻,A是静止的,A离开质心C的距离为lA,A的平衡位置离开质心的距离为![]() 故此时A离开平衡位置的距离即为振幅AA,
故此时A离开平衡位置的距离即为振幅AA,
![]()
而此时![]() ,故
,故
![]()
由此得
![]() (22)
(22)
在时刻t,A在地面参考系中的坐标

解法二:
当![]() 球相对于地面参考系的坐标为
球相对于地面参考系的坐标为![]() 时,弹簧
时,弹簧![]() 的伸长量为
的伸长量为![]() ,
,![]() 所受的合力为
所受的合力为
![]()
其加速度为
![]()
![]()
其相对于质心的加速度为
![]()
其中![]() 表示
表示![]() 球相对于其平衡位置的位移,在相互平动的两个参考系中,相对位移与参考系无关.
球相对于其平衡位置的位移,在相互平动的两个参考系中,相对位移与参考系无关.
上式表明,相对质心,![]() 球的加速度与其相对于平衡位置的位移成正比且反向.也就是说,
球的加速度与其相对于平衡位置的位移成正比且反向.也就是说,![]() 球相对质心作简谐振动.
球相对质心作简谐振动.
同理可证,
![]()
![]()
![]()
其相对于质心的加速度为
![]()
![]()
其中![]() 表示
表示![]() 球相对于其平衡位置的位移,相对质心,
球相对于其平衡位置的位移,相对质心,![]() 球的加速度与其相对于平衡位置的位移成正比且反向,即
球的加速度与其相对于平衡位置的位移成正比且反向,即![]() 球相对质心也作简谐振动.且有
球相对质心也作简谐振动.且有![]() 与
与![]() 振动的圆频率相等,
振动的圆频率相等,
![]()
![]()
天星 教育网
解法三:
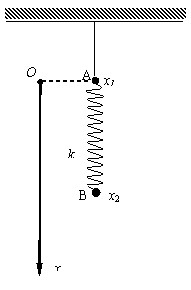
在地面参考系中,列A、B的牛顿定律方程
![]()
![]()
2![]()
![]()
x1、x2是A、B的坐标,l0是弹簧的自然长.
![]() 时,有
时,有
![]()
![]()
![]() 为初始时即细线刚烧断时刻,弹簧的长度,有关系
为初始时即细线刚烧断时刻,弹簧的长度,有关系
![]()
所以
![]()
由![]() +
+![]() ,
,
![]()
令![]() ,
,![]() 是一个恒定的加速度,结合初始条件,
是一个恒定的加速度,结合初始条件,![]() 对应的坐标和运动方程是,
对应的坐标和运动方程是,
![]()
![]()
再由![]()
![]()
![]() ,
,
![]()
![]()
这是一个以A为参考系描写B物体运动的动力学方程,且是简谐的,所以直接写出解答,
![]()
结合初条件,
![]()
![]()
得到
![]()
![]()
所以
![]()
即
![]()
![]()
由![]()
![]()
![]() ,得
,得
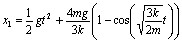
![]()
由![]() +
+![]() ,得
,得
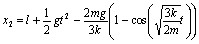
![]()

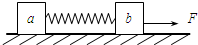
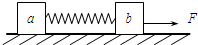 如图所示,在水平面上放着两个木块a和b,质量分别为ma、mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a、b以相同的速度做匀速直线运动,弹簧的伸长量为x.则下列关系正确的是( )
如图所示,在水平面上放着两个木块a和b,质量分别为ma、mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a、b以相同的速度做匀速直线运动,弹簧的伸长量为x.则下列关系正确的是( ) 如图所示,在水平面上放着两个木块a和b,质量分别为ma、mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a、b以相同的速度做匀速直线运动,弹簧的伸长量为x.则下列关系正确的是
如图所示,在水平面上放着两个木块a和b,质量分别为ma、mb,它们与水平面间的动摩擦因数为μ.两木块之间连接一个劲度系数为k的轻弹簧,弹簧原长为L.对b施加水平向右的拉力F,a、b以相同的速度做匀速直线运动,弹簧的伸长量为x.则下列关系正确的是