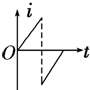题目内容
15.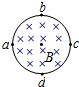 如图所示,a、b、c、d为导体圆环的四等分点,圆环的半径为R,一匀强磁场垂直于圆环平面,且磁场的磁感应强度随时间变化规律满足B=kt,则a、b两点间的电压为( )
如图所示,a、b、c、d为导体圆环的四等分点,圆环的半径为R,一匀强磁场垂直于圆环平面,且磁场的磁感应强度随时间变化规律满足B=kt,则a、b两点间的电压为( )| A. | 0 | B. | $\frac{{πk{R^2}}}{4}$ | C. | $\frac{{3πk{R^2}}}{4}$ | D. | πkR2 |
分析 先根据法拉第电磁感应定律列式求解感应电动势,本题的电动势是感生电动势,是涡旋电场产生的;然后根据欧姆定律求解感应电流,根据U=E-Ir求解任意两点间的电势差即可.
解答 解:根据法拉第电磁感应定律,有:
E=n$\frac{△∅}{△t}$=nS$\frac{△B}{△t}$=nπR2k
感应电流为:
I=$\frac{E}{{r}_{总}}$
则a、b两点间的电压为:
Uab=Eab-Irab=$\frac{E}{4}-I•\frac{{r}_{总}}{4}$=$\frac{1}{4}$nπR2k-$\frac{nπ{R}^{2}k}{{r}_{总}}$•$\frac{{r}_{总}}{4}$=0
故选:A
点评 本题关键是明确感应电动势是涡旋电场驱动产生,然后结合闭合电路欧姆定律、法拉第电磁感应定律列式求解,注意本题中任意两个点间的电势差均为零,不难.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案
相关题目
5.有一单摆,在海平面上某一段时间内摆动了N次,在该处某山顶上同样长的时间内摆动了N-1次,由此可知,此山的海拨高度是地球半径的( )
| A. | $\frac{1}{N-1}$倍 | B. | $\frac{1}{N}$倍 | C. | $\frac{1}{N+1}$倍 | D. | $\frac{N-1}{N+1}$倍 |
6.下列说法正确的是( )
| A. | 日心说的代表人物是哥白尼 | |
| B. | 太阳是静止不动的,地球和其他行星绕太阳转动 | |
| C. | 地球是绕太阳运动的一颗行星 | |
| D. | 日心说和地心说都是错误的 |
10.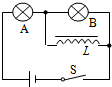 如图所示,A、B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键S闭合,等到灯泡亮度稳定后,下列说法正确的是( )
如图所示,A、B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键S闭合,等到灯泡亮度稳定后,下列说法正确的是( )
 如图所示,A、B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键S闭合,等到灯泡亮度稳定后,下列说法正确的是( )
如图所示,A、B是两个完全相同的灯泡,L是自感系数较大的线圈,其直流电阻忽略不计.当电键S闭合,等到灯泡亮度稳定后,下列说法正确的是( )| A. | 电键S断开时,A立即熄灭,而B会亮一下后才熄灭 | |
| B. | 电键S断开时,B立即熄灭,而A会亮一下后才熄灭 | |
| C. | 电键S闭合时,A、B同时亮,然后A熄灭 | |
| D. | 电键S闭合时,A、B同时亮,然后B逐渐变暗,直到不亮,A更亮 |
20.关于电磁感应,下列说法正确的是( )
| A. | 穿过闭合导体回路的磁通量越大,电路中的感应电流就越大 | |
| B. | 穿过闭合电路的磁通量变化越快,电路中的感应电动势越大 | |
| C. | 只要闭合线圈中磁通量不为零,就会有感应电流产生 | |
| D. | 线圈中的磁通量变化越大,电路中的感应电动势越大 |
4.发现行星运动规律和万有引力定律的科学家分别是( )
| A. | 伽利略、开普勒 | B. | 开普勒、牛顿 | C. | 牛顿、卡文迪许 | D. | 伽利略、牛顿 |
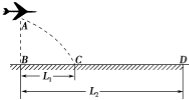 如图所示,在水平地面上空有一架飞机在进行投弹训练,飞机沿水平方向做匀加速直线运动.当飞机飞经观察点B点正上方A点时投放一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时飞机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.求:
如图所示,在水平地面上空有一架飞机在进行投弹训练,飞机沿水平方向做匀加速直线运动.当飞机飞经观察点B点正上方A点时投放一颗炸弹,经时间T炸弹落在观察点B正前方L1处的C点,与此同时飞机投放出第二颗炸弹,最终落在距观察点B正前方L2处的D点,且L2=3L1,空气阻力不计.求: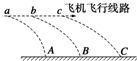 如图所示,在距地面80m高的水平面上做匀加速直线运动的飞机上每隔1s依次放下a、b、c三物体,抛出点a、b与b、c间距分别为45m和55m,分别落在水平地面上的A、B、C处.g=10m/s2
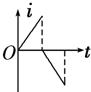
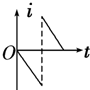
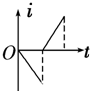
如图所示,在距地面80m高的水平面上做匀加速直线运动的飞机上每隔1s依次放下a、b、c三物体,抛出点a、b与b、c间距分别为45m和55m,分别落在水平地面上的A、B、C处.g=10m/s2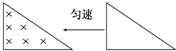 如图所示,一直角三角形金属框,向左匀速地穿过一个方向垂直于纸面向内的匀强磁场,磁场仅限于三角形边界所围的区域内,该区域的形状与金属框完全相同,且金属框的下边与磁场区域的下边在一条直线上.若取顺时针方向为电流的正方向,则金属框穿过磁场过程的感应电流i随时间t变化的图象是下图所示的( )
如图所示,一直角三角形金属框,向左匀速地穿过一个方向垂直于纸面向内的匀强磁场,磁场仅限于三角形边界所围的区域内,该区域的形状与金属框完全相同,且金属框的下边与磁场区域的下边在一条直线上.若取顺时针方向为电流的正方向,则金属框穿过磁场过程的感应电流i随时间t变化的图象是下图所示的( )