题目内容
【题目】假设宇宙中有两颗相距足够远的行星A和B，半径分别为
和
。各自相应的两颗卫足环绕行星运行周期的平方(门与轨道半径的三次方(所的关系如图所示，两颗卫星环绕相应行星表而运行的周期都为
。则
A. 行星A的质量大于行星B的质量
B. 行星A的密度小于行星B的密度
C. 行星A的第一宇宙速度等于行星B的第一字宙速度
D. 当两行星的卫星轨道半径相同时，行星A的卫星向心加速度大于行星B的卫星向心加速度
【答案】AD
【解析】试题分析：根据万有引力提供向心力得出中心天体质量得表达式，结合图象判断质量大小，根图象可知，在两颗行星表面做匀速圆周运动的周期相同，根据密度公式判断密度大小，根据
判断第一宇宙速度大小，根据
得a的表达式，进而比较向心加速度大小．
根据万有引力提供向心力得
，解得
，从图中可知斜率越小，
越大，质量越大，所以行星A的质量大于行星B的质量，A正确；根图象可知，在两颗行星表面做匀速圆周运动的周期相同，密度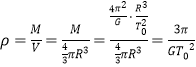
，所以行星A的密度等于行星B的密度，B错误；第一宇宙速度，A的半径大于B的半径，卫星环绕行星表面运行的周期相同，则A的第一宇宙速度大于行星B的第一宇宙速度，C错误；根据得
，当两行星的卫星轨道半径相同时，A的质量大于B的质量，则行星A的卫星向心加速度大于行星B的卫星向心加速，D正确．
练习册系列答案
阅读快车系列答案
相关题目
