题目内容
17.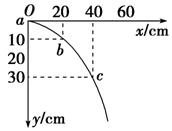 某同学在做平抛运动实验得出如图所示的小球运动轨迹,a、b、c三点的位置在运动轨迹上已标出.则:(g取10m/s2)
某同学在做平抛运动实验得出如图所示的小球运动轨迹,a、b、c三点的位置在运动轨迹上已标出.则:(g取10m/s2)(1)小球平抛的初速度为2m/s.
(2)小球开始做平抛运动的位置坐标为x=-10cm,y=-1.25cm.
(3)小球运动到b点的速度为2.5m/s.
分析 平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动,根据竖直方向上△y=gT2,求出时间间隔,再根据水平方向上的匀速直线运动求出初速度.
求出b点在竖直方向上的速度,即可求出运动的时间和b点速度,从而求出此时小球水平方向和竖直方向上的位移,即可求出抛出点的坐标.
解答 解:(1)在竖直方向上△y=gT2,T=$\sqrt{\frac{△y}{g}}$=$\sqrt{\frac{0.20-0.10}{10}}$=0.1s.则小球平抛运动的初速度v0=$\frac{x}{T}=\frac{0.2}{0.1}$m/s=2m/s.
(2)b点在竖直方向上的分速度vby=$\frac{{y}_{ac}}{2T}$=$\frac{0.3}{0.2}$=1.5m/s,
则运动的时间t=$\frac{{v}_{by}}{g}$=$\frac{1.5}{10}$=0.15s.
水平方向上的位移x1=vt=0.3m,竖直方向上的位移y=$\frac{1}{2}$gt2=$\frac{1}{2}×10×0.1{5}^{2}$=0.1125m.
所以开始做平抛运动的位置坐标x=0.2-0.3=-0.1m=-10cm,y=0.1-0.1125=-0.0125m=-1.25cm
(3)小球运动到b点的速度为v=$\sqrt{{{v}_{0}}^{2}+{{v}_{By}}^{2}}$=$\sqrt{{2}^{2}+1.{5}^{2}}$=2.5m/s
故答案为:(1)2; (2)-10,-1.25; (3)2.5
点评 解决本题的关键知道平抛运动在水平方向上做匀速直线运动,在竖直方向上做自由落体运动.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.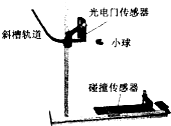 如图,研究平抛运动规律的实验装置放置在水平桌面上,利用光电门传感器和碰撞传感器可测得小球的水平初速度和飞行时间,底板上的标尺可以测得水平位移.
如图,研究平抛运动规律的实验装置放置在水平桌面上,利用光电门传感器和碰撞传感器可测得小球的水平初速度和飞行时间,底板上的标尺可以测得水平位移.
保持水平槽口距底板高度h=0.420m不变.改变小球在斜槽导轨上下滑的起始位置,测出小球做平抛运动的初速度v0、飞行时间t和水平位移d,记录在表中.
(1)由表中数据可知,在h一定时,小球水平位移d与其初速度v0成正比关系.
(2)一位同学计算出小球飞行时间的理论值t理=$\sqrt{\frac{2h}{g}}$=$\sqrt{\frac{2×0.420}{10}}$=289.8m/s,发现理论值与测量值之差约为3ms.经检查,实验及测量无误,其原因是g取值10m/s2偏大.
(3)另一位同学分析并纠正了上述偏差后,改变槽口离底板的高度h,另做了几次实验,竞发现测量值t′依然大于自己得到的理论值t理′,但二者之差在3-7ms之间,且高度越大差值越大.对实验装置的安装进行检查,确认斜槽槽口与底座均水平,则导致偏差的原因是光电门传感器位于水平槽口的内侧,传感器的中心距离水平槽口(小球开始做平抛运动的位置)还有一段很小的距离.
 如图,研究平抛运动规律的实验装置放置在水平桌面上,利用光电门传感器和碰撞传感器可测得小球的水平初速度和飞行时间,底板上的标尺可以测得水平位移.
如图,研究平抛运动规律的实验装置放置在水平桌面上,利用光电门传感器和碰撞传感器可测得小球的水平初速度和飞行时间,底板上的标尺可以测得水平位移.保持水平槽口距底板高度h=0.420m不变.改变小球在斜槽导轨上下滑的起始位置,测出小球做平抛运动的初速度v0、飞行时间t和水平位移d,记录在表中.
(1)由表中数据可知,在h一定时,小球水平位移d与其初速度v0成正比关系.
| v0(m/s) | 0.741 | 1.034 | 1.318 | 1.584 |
| t(ms) | 292.7 | 293.0 | 292.8 | 292.9 |
| d(cm) | 21.7 | 30.3 | 38.6 | 46.4 |
(3)另一位同学分析并纠正了上述偏差后,改变槽口离底板的高度h,另做了几次实验,竞发现测量值t′依然大于自己得到的理论值t理′,但二者之差在3-7ms之间,且高度越大差值越大.对实验装置的安装进行检查,确认斜槽槽口与底座均水平,则导致偏差的原因是光电门传感器位于水平槽口的内侧,传感器的中心距离水平槽口(小球开始做平抛运动的位置)还有一段很小的距离.
8.做初速度不为零的匀加速直线运动的物体,在时间T内通过位移s1到达A点,接着在时间T内又通过位移s2到达B点,则以下判断正确的是( )
| A. | 物体在B点的速度大小为$\frac{{s}_{1}+{s}_{2}}{2T}$ | B. | 物体运动的加速度为$\frac{2{s}_{1}}{{T}^{2}}$ | ||
| C. | 物体运动的加速度为$\frac{{s}_{2}-{s}_{1}}{{T}^{2}}$ | D. | 物体在B点的速度大小为$\frac{2{s}_{2}-{s}_{1}}{T}$ |
5. “碰撞中的动量守恒”实验中,仪器按要求安装好后开始实验,第一次不放被碰小球,第二次把被碰小球直接静止放在斜槽末端的水平部分,在白纸上记录下重锤位置和各小球落点的平均位置依次为O、A、B、C,设入射小球和被碰小球的质量依次为m1、m2,则下列说法中正确的有( )
“碰撞中的动量守恒”实验中,仪器按要求安装好后开始实验,第一次不放被碰小球,第二次把被碰小球直接静止放在斜槽末端的水平部分,在白纸上记录下重锤位置和各小球落点的平均位置依次为O、A、B、C,设入射小球和被碰小球的质量依次为m1、m2,则下列说法中正确的有( )
 “碰撞中的动量守恒”实验中,仪器按要求安装好后开始实验,第一次不放被碰小球,第二次把被碰小球直接静止放在斜槽末端的水平部分,在白纸上记录下重锤位置和各小球落点的平均位置依次为O、A、B、C,设入射小球和被碰小球的质量依次为m1、m2,则下列说法中正确的有( )
“碰撞中的动量守恒”实验中,仪器按要求安装好后开始实验,第一次不放被碰小球,第二次把被碰小球直接静止放在斜槽末端的水平部分,在白纸上记录下重锤位置和各小球落点的平均位置依次为O、A、B、C,设入射小球和被碰小球的质量依次为m1、m2,则下列说法中正确的有( )| A. | 第一、二次入射小球的落点依次是A、B | |
| B. | B到O点的距离长短与实验中选用小球的质量大小有关 | |
| C. | m1$\overline{OB}$=m2$\overline{OA}$+m1$\overline{OC}$ | |
| D. | m1$\overline{OB}$=m1$\overline{OA}$+m2$\overline{OC}$ |
2.如果在北京和广州各放一个物体随地球自转做匀速圆周运动,则这两个物体具有大小相同的是( )
| A. | 线速度 | B. | 角速度 | C. | 加速度 | D. | 向心力 |
9.由交流电动势瞬时值表达式e=10$\sqrt{2}$sin4πt(V),可知( )
| A. | 此交流电的频率是4π(Hz) | |
| B. | 此交流电的周期是0.5s | |
| C. | 当t=0时,产生此交流电的线圈平面与中性面重合 | |
| D. | 当t=0.5s时,此交流电动势有最大值 |
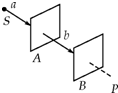 如图所示,电灯S发出的光先后经过偏振片A和B,人眼在P处迎着入射光方向,看不到光亮,则图中a光为自然光.图中b光为偏振光.以SP为轴将B转过180°后,在P处不能(选填“能”或“不能”)看到光亮,以SP为轴将B转过90°后,在P处能(选填“能”或“不能”)看到光亮.
如图所示,电灯S发出的光先后经过偏振片A和B,人眼在P处迎着入射光方向,看不到光亮,则图中a光为自然光.图中b光为偏振光.以SP为轴将B转过180°后,在P处不能(选填“能”或“不能”)看到光亮,以SP为轴将B转过90°后,在P处能(选填“能”或“不能”)看到光亮.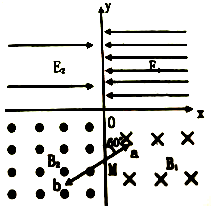 在xOy平面第Ⅰ象限中,存在沿x轴负方向的匀强电场,场强为E1=$\frac{3πBl}{2{t}_{0}}$,第Ⅱ象限中存在沿x轴正方向的匀强电场,场强为E2=$\frac{πBl}{2{t}_{0}}$,在第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,方向如图所示.磁感应强度B1=B,B2=2B.带电粒子a、b同时从y轴上的点M(0,-$\sqrt{3}$l)以不同的速率向相反方向射出,射出时粒子a的速度方向与y轴正方向成60°角,经过时间t0,粒子a、b同时第一次垂直x轴进入电场,不计粒子重力和两粒子间相互作用.求:
在xOy平面第Ⅰ象限中,存在沿x轴负方向的匀强电场,场强为E1=$\frac{3πBl}{2{t}_{0}}$,第Ⅱ象限中存在沿x轴正方向的匀强电场,场强为E2=$\frac{πBl}{2{t}_{0}}$,在第Ⅲ、Ⅳ象限中,存在垂直于xOy平面方向的匀强磁场,方向如图所示.磁感应强度B1=B,B2=2B.带电粒子a、b同时从y轴上的点M(0,-$\sqrt{3}$l)以不同的速率向相反方向射出,射出时粒子a的速度方向与y轴正方向成60°角,经过时间t0,粒子a、b同时第一次垂直x轴进入电场,不计粒子重力和两粒子间相互作用.求: