题目内容
8. 如图所示,平面坐标系Oxy中,在y>0的区域存在沿y轴负方向的匀强电场,场强大小为E,在-h<y<0的区域Ⅰ中存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在y<-h的区域Ⅱ中存在垂直纸面向里的匀强磁场,磁感应强度大小为2B.A是y轴上的一点,C是x轴上的一点.一质量为m、电荷量为q的带正电的粒子以某一初速度沿x轴正方向从A点进入电场区域,继而通过C点以速度方向与x轴夹角为φ=30°进入磁场区域Ⅰ,并以垂直边界y=-h的速度进入磁场区域Ⅱ.粒子重力不计.试求:
如图所示,平面坐标系Oxy中,在y>0的区域存在沿y轴负方向的匀强电场,场强大小为E,在-h<y<0的区域Ⅰ中存在垂直纸面向外的匀强磁场,磁感应强度大小为B,在y<-h的区域Ⅱ中存在垂直纸面向里的匀强磁场,磁感应强度大小为2B.A是y轴上的一点,C是x轴上的一点.一质量为m、电荷量为q的带正电的粒子以某一初速度沿x轴正方向从A点进入电场区域,继而通过C点以速度方向与x轴夹角为φ=30°进入磁场区域Ⅰ,并以垂直边界y=-h的速度进入磁场区域Ⅱ.粒子重力不计.试求:(1)粒子经过C点时的速度大小v;
(2)A、C两点与O点间的距离y0、x0;
(3)粒子从A点出发,经过多长时间可回到y=y0处?
分析 (1)粒子在磁场Ⅰ中做匀速圆周运动,由几何知识知,轨迹对应的圆心角为60°,根据几何关系求得轨迹半径,根据牛顿第二定律列式求速度大小.
(2)粒子在电场中做类平抛运动,运用运动的分解,由牛顿第二定律和运动学公式结合可求得A、C两点与O点间的距离y0、x0;
(3)分段求时间,磁场中找出轨迹对应的圆心角θ,由t=$\frac{θ}{2π}$T求粒子第一次返回y=y0处前运动的总时间T,根据周期性,粒子返回y=y0处前运动的总时间为t=nT
解答 解:(1)由题可知,粒子在磁场Ⅰ中做匀速圆周运动的圆心角θ=60°,相应的半径为
${r_1}=\frac{h}{sin60°}=\frac{{2\sqrt{3}}}{3}h$
由$qvB=m\frac{v^2}{r_1}$,得
$v=\frac{{2\sqrt{3}qBh}}{3m}$
(2)粒子在电场中做类平抛运动,有
x0=vcos30°•t0
${y_0}=\frac{1}{2}•\frac{Eq}{m}•{t_0}^2$
又$vsin30°=\frac{Eq}{m}•{t_0}$
解得,${t_0}=\frac{{\sqrt{3}Bh}}{3E}$,${x_0}=\frac{{\sqrt{3}{B^2}{h^2}q}}{3mE}$,${y_0}=\frac{{{B^2}{h^2}q}}{6mE}$;
(3)根据运动的对称性可知,第一次返回y=y0处前在磁场Ⅰ中运动的总时间为${t_1}=\frac{2π}{3}•\frac{m}{qB}$
在磁场Ⅱ中运动的总时间为${t_2}=\frac{π}{2}•\frac{m}{qB}$
故第一次返回y=y0处前运动的总时间为$T=2{t_0}+{t_1}+{t_2}=\frac{{2\sqrt{3}Bh}}{3E}+\frac{7π}{6}•\frac{m}{qB}$
之后运动呈周期性,故返回y=y0处前运动的总时间为$t=nT=n(\frac{{2\sqrt{3}Bh}}{3E}+\frac{7π}{6}•\frac{m}{qB}),n∈N$
答:(1)粒子经过C点时的速度大小为$\frac{2\sqrt{3}qBh}{3m}$;
(2)A、C两点与O点间的距离y0、x0分别为$\frac{\sqrt{3}{B}^{2}{h}^{2}q}{3mE}$,$\frac{{B}^{2}{h}^{2}q}{6mE}$;
(3)粒子从A点出发,经过$t=nT=n(\frac{{2\sqrt{3}Bh}}{3E}+\frac{7π}{6}•\frac{m}{qB}),n∈N$可回到y=y0处.
点评 本题考查带电粒子在电磁场中的运动,注意在磁场中的运动要注意几何关系的应用,在电场中注意由类平抛运动的规律求解.

| A. | 光具有粒子性 | B. | 光是电磁波 | C. | 光是一种横波 | D. | 光是一种纵波 |
 在不少旅游景点里都设置了一种速降的游乐项目,从山上高处向山下低处安装一根钢索,人坐在吊篮里通过绳索和滑轮保持相对静止一起沿着倾角为θ的钢索快速下滑,如图所示,绳索与竖直方向间的夹角α,则下列说法正确的是( )
在不少旅游景点里都设置了一种速降的游乐项目,从山上高处向山下低处安装一根钢索,人坐在吊篮里通过绳索和滑轮保持相对静止一起沿着倾角为θ的钢索快速下滑,如图所示,绳索与竖直方向间的夹角α,则下列说法正确的是( )| A. | 若α>θ,则人和吊篮至少受3个力的作用 | |
| B. | 若α>θ,则整个装置的加速度一定大于gsinθ | |
| C. | 若α=θ,则整个装置的加速度一定为gsinθ | |
| D. | 因为整个装置的加速度不可能大于gsinθ,所以α>θ不可能的 |
| A. | 突变型光纤的从光纤中心芯到玻璃包层的折射率是突然变大 | |
| B. | 渐变型光纤的从光纤中心芯到玻璃包层的折射率是逐渐变小 | |
| C. | 光在渐变型光纤中的传播轨迹是直折线 | |
| D. | 光在突变型光纤中的传播轨迹是曲线 |
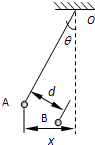 某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )
某老师用图示装置探究库仑力与电荷量的关系.A、B是可视为点电荷的两带电小球,用绝缘细线将A悬挂,实验中在改变电荷量时,移动B并保持A、B连线与细线垂直.用Q和q表示A、B的电荷量,d表示A、B间的距离,θ(θ不是很小)表示细线与竖直方向的夹角,x表示A偏离O点的水平距离.实验中( )| A. | d应保持不变 | B. | B的位置在同一圆弧上 | ||
| C. | x与电荷量乘积Qq成正比 | D. | tanθ与A、B间库仑力成正比 |
 如图所示,两平行金属板水平放置,与电源相连,开始开关S闭合使平行板电容器带电,两平行金属板间存在匀强磁场,一个不计重力的带电粒子以速度v0垂直电场从P点射入平行板间,恰好沿纸面做匀速直线运动,从Q点飞出,下列说法正确的是( )
如图所示,两平行金属板水平放置,与电源相连,开始开关S闭合使平行板电容器带电,两平行金属板间存在匀强磁场,一个不计重力的带电粒子以速度v0垂直电场从P点射入平行板间,恰好沿纸面做匀速直线运动,从Q点飞出,下列说法正确的是( )| A. | 磁感应强度方向垂直纸面向外 | |
| B. | 保持开关闭合,把两板的距离增大一倍,同时把板间的磁感应强度增大一倍,带电粒子仍沿水平直线PQ飞出 | |
| C. | 如果粒子带正电,以另一速度v1从P点沿PQ射入,从Q′点飞出,则v1<v0 | |
| D. | 若把开关S断开,两板的距离减小一半,带电粒子仍沿水平直线PQ飞出 |
 平抛运动演示器如图所示,开始时完全相同的A、B两球均静止在离水平地面h高处,当用小锤击打弹性金属片C时,A球沿水平方向飞出,做平抛运动;与此同时,B球被松开做自由落体运动.落地时A、B两球相距为s.已知h=1.25m,s=0.5m,重力加速度g=10m/s2.,不计空气阻力.问:
平抛运动演示器如图所示,开始时完全相同的A、B两球均静止在离水平地面h高处,当用小锤击打弹性金属片C时,A球沿水平方向飞出,做平抛运动;与此同时,B球被松开做自由落体运动.落地时A、B两球相距为s.已知h=1.25m,s=0.5m,重力加速度g=10m/s2.,不计空气阻力.问: