题目内容
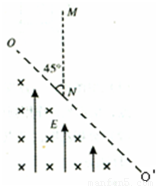
如图所示,有一与竖直方向夹角为45°的直线边界,其左下方有一正交的匀强电磁场,磁场方向垂直于纸面向里,磁感应强度B= T;电场方向竖直向上,场强
T;电场方向竖直向上,场强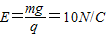 ,一质量为m=2×10-5kg,电荷量q=+2×10-5C的小球从边界上N点正上方高为h=0.2m处的M点静止释放,下落到N点时小球瞬间爆炸成质量、电荷量均相等的A、B两块,已知爆炸后A向上运动,能达到的最大高度为4h;B向下运动进入电磁场区域,此后A也将进入电磁场区域.g=10m/s2
,一质量为m=2×10-5kg,电荷量q=+2×10-5C的小球从边界上N点正上方高为h=0.2m处的M点静止释放,下落到N点时小球瞬间爆炸成质量、电荷量均相等的A、B两块,已知爆炸后A向上运动,能达到的最大高度为4h;B向下运动进入电磁场区域,此后A也将进入电磁场区域.g=10m/s2求:
(1)B刚进入电磁场区域的速度v1?
(2)B第二次进入电磁场区域的速度v2?
(3)设B、A第二次进入电磁场时,与边界OO'交点分别为P、Q,求PQ之间的距离.
【答案】分析:(1)根据动能定理,结合动量守恒定律求出B刚进入电磁场区域的速度.
(2)B进入电磁场,受到的电场力和重力相等,做匀速圆周运动,根据几何关系,得出B出磁场后的速度方向,从而确定其运动情况,从而根据运动分析得出第二次进入电磁场的速度.
(3)根据圆周运动的知识,结合轨道半径,运用几何关系分别求出A、B第二次进入电磁场与第一次进入电磁场之间的距离,从而求出PQ之间的距离.
解答:解:(1)根据动能定理得,mgh=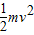
解得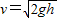 .
.
规定向下为正方向,
爆炸的瞬间系统动量守恒,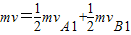
爆炸后A向上运动,能上升的最大高度为4h,则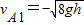 .
.
B刚进入电磁场区域的速度v1=vB1=8m/s.
(2)对B:进入磁场后,由于qE=mg,所以做匀速圆周运动.
由几何关系知,B离开电磁场做平抛运动.
s=v1t
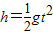
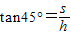
解得:t=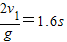 .
.
B第二次进入电磁场区域: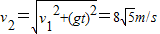
方向与水平方向的夹角tanα=2.
(3)对B:第一次进入电磁场做匀速圆周运动.
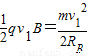 ,解得:
,解得: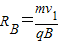 .
.
B第二次进入电磁场与第一次进入电磁场的距离NP.
NP=NC+CP=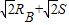 .
.
同理,A第二次进入电磁场与第一次进入电磁场的距离为NQ.
NQ=ND+DQ=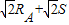 1.
1.
PQ=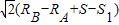 =
=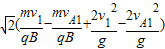 =12
=12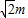 .
.
答:(1)B刚进入电磁场区域的速度为8m/s.
(2)B第二次进入电磁场区域的速度为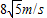 .
.
(3)PQ之间的距离为12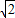 m.
m.
点评:本题综合运用了动能定理、动量守恒定律、牛顿第二定律,综合性较强,对数学几何能力的要求较高,关键搞清A、B的运动情况,选择合适的规律进行求解.
(2)B进入电磁场,受到的电场力和重力相等,做匀速圆周运动,根据几何关系,得出B出磁场后的速度方向,从而确定其运动情况,从而根据运动分析得出第二次进入电磁场的速度.
(3)根据圆周运动的知识,结合轨道半径,运用几何关系分别求出A、B第二次进入电磁场与第一次进入电磁场之间的距离,从而求出PQ之间的距离.
解答:解:(1)根据动能定理得,mgh=
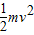
解得
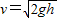 .
.规定向下为正方向,
爆炸的瞬间系统动量守恒,
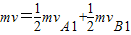
爆炸后A向上运动,能上升的最大高度为4h,则
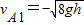 .
.B刚进入电磁场区域的速度v1=vB1=8m/s.
(2)对B:进入磁场后,由于qE=mg,所以做匀速圆周运动.
由几何关系知,B离开电磁场做平抛运动.
s=v1t
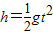
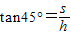
解得:t=
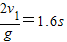 .
.B第二次进入电磁场区域:
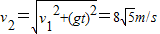
方向与水平方向的夹角tanα=2.
(3)对B:第一次进入电磁场做匀速圆周运动.
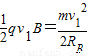 ,解得:
,解得: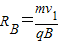 .
.B第二次进入电磁场与第一次进入电磁场的距离NP.
NP=NC+CP=
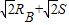 .
.同理,A第二次进入电磁场与第一次进入电磁场的距离为NQ.
NQ=ND+DQ=
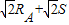 1.
1.PQ=
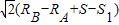 =
=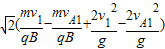 =12
=12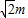 .
.答:(1)B刚进入电磁场区域的速度为8m/s.
(2)B第二次进入电磁场区域的速度为
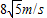 .
.(3)PQ之间的距离为12
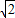 m.
m.点评:本题综合运用了动能定理、动量守恒定律、牛顿第二定律,综合性较强,对数学几何能力的要求较高,关键搞清A、B的运动情况,选择合适的规律进行求解.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
 如图所示,有一与竖直方向夹角为45°的直线边界,其左下方有一正交的匀强电磁场,磁场方向垂直于纸面向里,磁感应强度B=
如图所示,有一与竖直方向夹角为45°的直线边界,其左下方有一正交的匀强电磁场,磁场方向垂直于纸面向里,磁感应强度B= (2009?黄州区模拟)如图所示,有一与竖直方向夹角为45°的直线边界,其左下方有一正交的匀强电磁场.磁场方向垂直于纸面向里,磁感应强度大小为B;电场方向竖直向上,场强大小为E=mg/q.一质量为m,电荷量为+q的小球从边界上N点正上方高为h处的M点静止释放,下落到N点时小球瞬间爆炸成质量、电荷量均相等的A、B两块.已知爆炸后A向上运动,能达到的最大高度为4h;B向下运动进入电磁场区域.此后A也将进入电磁场区域,求:
(2009?黄州区模拟)如图所示,有一与竖直方向夹角为45°的直线边界,其左下方有一正交的匀强电磁场.磁场方向垂直于纸面向里,磁感应强度大小为B;电场方向竖直向上,场强大小为E=mg/q.一质量为m,电荷量为+q的小球从边界上N点正上方高为h处的M点静止释放,下落到N点时小球瞬间爆炸成质量、电荷量均相等的A、B两块.已知爆炸后A向上运动,能达到的最大高度为4h;B向下运动进入电磁场区域.此后A也将进入电磁场区域,求: (3)设B、A第二次进入电磁场时,与边界OO'交点分别为P、Q,求PQ之间的距离.
(3)设B、A第二次进入电磁场时,与边界OO'交点分别为P、Q,求PQ之间的距离. (3)设B、A第二次进入电磁场时,与边界OO'交点分别为P、Q,求PQ之间的距离.
(3)设B、A第二次进入电磁场时,与边界OO'交点分别为P、Q,求PQ之间的距离. (3)设B、A第二次进入电磁场时,与边界OO'交点分别为P、Q,求PQ之间的距离.
(3)设B、A第二次进入电磁场时,与边界OO'交点分别为P、Q,求PQ之间的距离.