题目内容
16.如图所示为一次记录小车运动情况的纸带,图中A、B、C、D、E、F、G为相邻的计数点,相邻计数点间有4个点未画出
(1)相邻计数点间的时间间隔T=0.1s
(2)计数点D对应的速度大小是0.26m/s
(3)小车运动的加速度的大小是0.50m/s2(计算结果保留两位有效数字).
分析 根据某段时间内的平均速度等于中间时刻的瞬时速度求出计数点D的瞬时速度,根据连续相等时间内的位移之差是一恒量求出小车的加速度.
解答 解:(1)打点的时间周期为0.02s,因为相邻计数点间有4个点未画出,则相邻计数点间的时间间隔为0.1s.
(2)计数点D对应的瞬时速度${v}_{D}=\frac{{x}_{CE}}{2T}=\frac{(2.38+2.88)×1{0}^{-2}}{0.2}$m/s=0.26m/s.
(3)根据△x=aT2,运用逐差法得,$a=\frac{{x}_{DG}-{x}_{AD}}{9{T}^{2}}$=$\frac{(2.88+3.39+3.87-1.40-1.90-2.38)×1{0}^{-2}}{9×0.01}$=0.50m/s2
故答案为:(1)0.1s (2)0.26 (3)0.50.
点评 解决本题的关键掌握纸带的处理方法,会通过纸带求解瞬时速度和加速度,关键是匀变速直线运动推论的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.下列单位中属于国际单位制的基本单位的是( )
| A. | 秒 | B. | 牛顿 | C. | 焦耳 | D. | 米每秒 |
11. 如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗地球卫星,a、b质量相同,且小于c的质量,则下列说法正确的是( )
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗地球卫星,a、b质量相同,且小于c的质量,则下列说法正确的是( )
 如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗地球卫星,a、b质量相同,且小于c的质量,则下列说法正确的是( )
如图所示,a、b、c是地球大气层外圆形轨道上运行的三颗地球卫星,a、b质量相同,且小于c的质量,则下列说法正确的是( )| A. | b所需向心力最小 | |
| B. | 因为b、c的线速度小于a的线速度,所以卫星a变轨到卫星b、c所在轨道要减速 | |
| C. | b、c的向心加速度相等,且大于a的向心加速度 | |
| D. | b、c的周期相等,且大于a的周期 |
1.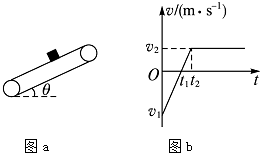 已知一足够长的传送带与水平面的倾角为θ,以一定的速度匀速运动.某时刻在适当的位置放上具有一定传送带的物块(如图a所示),以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2).已知传送带的速度保持不变,物块的质量为m,物块与传送带间的动摩擦因数为μ,重力加速度为g.则下列判断正确的是( )
已知一足够长的传送带与水平面的倾角为θ,以一定的速度匀速运动.某时刻在适当的位置放上具有一定传送带的物块(如图a所示),以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2).已知传送带的速度保持不变,物块的质量为m,物块与传送带间的动摩擦因数为μ,重力加速度为g.则下列判断正确的是( )
 已知一足够长的传送带与水平面的倾角为θ,以一定的速度匀速运动.某时刻在适当的位置放上具有一定传送带的物块(如图a所示),以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2).已知传送带的速度保持不变,物块的质量为m,物块与传送带间的动摩擦因数为μ,重力加速度为g.则下列判断正确的是( )
已知一足够长的传送带与水平面的倾角为θ,以一定的速度匀速运动.某时刻在适当的位置放上具有一定传送带的物块(如图a所示),以此时为t=0时刻记录了小物块之后在传送带上运动速度随时间的变化关系,如图b所示(图中取沿斜面向上的运动方向为正方向,其中两坐标大小v1>v2).已知传送带的速度保持不变,物块的质量为m,物块与传送带间的动摩擦因数为μ,重力加速度为g.则下列判断正确的是( )| A. | 0~t1内,物块对传送带做负功 | |
| B. | 0~t1内,电动机消耗的功率为μmgcosθ•v2 | |
| C. | 物块与传送带间的动摩擦因数μ与倾角θ的关系是:μ<tan θ | |
| D. | 0~t2内,传送带克服摩擦力产生的热量为Q=μmgcosθ$({\frac{{{v_2}{t_2}+{v_1}{t_1}}}{2}})$ |
8. 如图所示,A、B两物体的重力分别是GA=4N,GB=5N.A用细绳悬挂在顶板上,B放在水平地面上,A、B间轻弹簧的弹力F=3N,则细绳中的弹力FT及物体B对地面的压力FN的可能值分别是( )
如图所示,A、B两物体的重力分别是GA=4N,GB=5N.A用细绳悬挂在顶板上,B放在水平地面上,A、B间轻弹簧的弹力F=3N,则细绳中的弹力FT及物体B对地面的压力FN的可能值分别是( )
 如图所示,A、B两物体的重力分别是GA=4N,GB=5N.A用细绳悬挂在顶板上,B放在水平地面上,A、B间轻弹簧的弹力F=3N,则细绳中的弹力FT及物体B对地面的压力FN的可能值分别是( )
如图所示,A、B两物体的重力分别是GA=4N,GB=5N.A用细绳悬挂在顶板上,B放在水平地面上,A、B间轻弹簧的弹力F=3N,则细绳中的弹力FT及物体B对地面的压力FN的可能值分别是( )| A. | 9N和0N | B. | 7N和2N | C. | 3N和6N | D. | 1N和8N |
5.关于弹力的说法,正确的是( )
| A. | 物质互相接触,就有弹力的相互作用 | |
| B. | 物体发生形变,就必然对别的物体产生力作用 | |
| C. | 由胡克定律可得:k=$\frac{F}{x}$,可知弹簧的劲度系数与弹力成正比,与形变量成反比 | |
| D. | 绳的拉力沿绳而指向绳收缩的方向 |
6.2012年沈阳市开通首条旅游观光巴士,其采用双层大巴,巴士上层是观光的最佳位置,游客上车后会向上层移动,此时,车的重心将( )
| A. | 向前上方移动 | B. | 向后上方移动 | C. | 向上移动 | D. | 不变 |

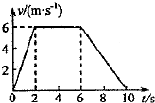 电梯从一楼开始向上运动,先匀加速上升了2s,再匀速上升4s,最后匀减速上升,10s末到达十五层后停止,这一过程中的v-t图如图所示,求:
电梯从一楼开始向上运动,先匀加速上升了2s,再匀速上升4s,最后匀减速上升,10s末到达十五层后停止,这一过程中的v-t图如图所示,求: