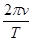题目内容
一行星绕恒星作圆周运动．由天文观测可得，其运动周期为T，速度为v，引力常量为G，则恒星的质量为 ，行星运动的轨道半径为 ．
分析：根据速度和周期的关系求出轨道半径，再根据万有引力提供向心力求出恒星的质量．
解答：解：根据v=
，所以r=
．
根据G
=mr(
)2得，M=
=
．
故答案为：
，
．
| 2πr |
| T |
| vT |
| 2π |
根据G
| Mm |
| r2 |
| 2π |
| T |
| 4π2r3 |
| GT2 |
| v3T |
| 2πG |
故答案为：
| v3T |
| 2πG |
| vT |
| 2π |
点评：解决本题的关键知道线速度与周期的关系，以及掌握万有引力提供向心力这一理论，会根据该理论求中心天体的质量．
练习册系列答案
相关题目
B．行星的质量为
D．行星运动的加速度为
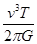B．行星的质量为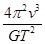
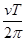D．行星运动的加速度为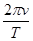
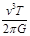B．行星的质量为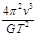
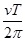D．行星运动的加速度为