题目内容
16.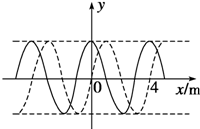 如图实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.求:
如图实线是某时刻的波形图象,虚线是经过0.2s时的波形图象.求:(1)可能的周期;
(2)可能的波速;
(3)若波速是35m/s,求波的传播方向;
(4)波传播的可能距离;
(5)当0.2s小于一个周期时,周期、波速、传播的距离.
分析 (1)该波可能向右传播,也可能向左传播,由时间与周期的关系和周期性求解.
(2)读出波长,由公式v=$\frac{λ}{T}$求可能的波速.
(3)将v=35m/s代入上题结果,分析波的传播方向.
(4)根据波的周期性和双向性,写出波传播的可能距离.
(5)当0.2s小于一个周期时,说明波在0.2 s内传播的距离小于一个波长.由上题结果求解.
解答 解:(1)若波向左传播,根据波形的周期性有:
0.2s=(n+$\frac{3}{4}$)T
可得:T=$\frac{0.8}{4n+3}$ s,(n=0、1、2、…)
若波向右传播,根据波形的周期性有:
0.2s=(n+$\frac{1}{4}$)T
可得:T=$\frac{0.8}{4n+1}$ s,(n=0、1、2、…)
(2)由图知波长 λ=4m
由v=$\frac{λ}{T}$得:若波向左传播,波速 v=(20n+15)m/s
若波向右传播,波速 v=(20n+5)m/s,(n=0、1、2、…).
(3)若波速是35m/s,符合v=(20n+15)m/s,故波向左传播.
(4)若波向左传播,根据波形的周期性有:
波传播的距离 x=(4n+3)m
若波向右传播,根据波形的周期性有:
波传播的距离 x=(4n+1)m,(n=0、1、2、…)
(5)若0.2 s小于一个周期,说明波在0.2 s内传播的距离小于一个波长.
则:向左传播时,传播的距离x=$\frac{3λ}{4}$=3 m;传播的时间t=$\frac{3T}{4}$,得
周期T=0.267 s;波速v=15 m/s.
向右传播时,传播的距离为$\frac{λ}{4}$=1 m;传播的时间t=$\frac{T}{4}$,得
周期T=0.8 s;波速v=5 m/s.
答:(1)可能的周期是 $\frac{0.8}{4n+3}$ s或$\frac{0.8}{4n+1}$ s(n=0、1、2、…).
(2)可能的波速是(20n+15)m/s或(2n+5)m/s,(n=0、1、2、…).
(3)波向左传播.
(4)波传播的可能距离是(4n+3)m或(4n+1)m,(n=0、1、2、…).
(5)若0.2 s小于一个周期,向左传播时,传播的距离是3 m,周期是0.267 s,波速是15 m/s.向右传播时,传播的距离为1 m,周期是0.8 s,波速是5 m/s.
点评 本题考查理解波动图象的能力以及运用数学通项求解特殊值的能力.对于两个时刻的波形,一定要考虑波的双向性和周期性.

 A、D分别是斜面的顶端和底端,B、C是斜面上的两个点,AB=BC=CD,E点在D点的正上方,与A等高.从E点以一定的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,关于球1和球2从抛出到落在斜面上的运动过程( )
A、D分别是斜面的顶端和底端,B、C是斜面上的两个点,AB=BC=CD,E点在D点的正上方,与A等高.从E点以一定的水平速度抛出质量相等的两个小球,球1落在B点,球2落在C点,关于球1和球2从抛出到落在斜面上的运动过程( )| A. | 球1和球2运动的时间之比为2:1 | |
| B. | 球1和球2运动的时间之比为1:$\sqrt{2}$ | |
| C. | 球1和球2抛出时初速度之比为2$\sqrt{2}$:1 | |
| D. | 球1和球2运动时的加速度之比为1:2 |
| A. | 四川汶川县发生8.0级强烈地震,地震波是机械波,其中既有横波也有纵波 | |
| B. | 不同频率的机械波在同一介质中传播时,传播速度不同 | |
| C. | 如果测量到来自遥远星系上某些元素发出的光波波长比地球上这些元素静止时发光的波长长,这说明该星系正在远离我们而去 | |
| D. | 全息照相是利用了光的干涉原理 |
 如图所示将一光滑的半圆槽置于光滑水平面上,槽的左侧有一固定在水平面上的物块.今让一小球自左侧槽口A的正上方从静止开始落下,与圆弧槽相切自A点进入槽内,则以下结论中正确的是( )
如图所示将一光滑的半圆槽置于光滑水平面上,槽的左侧有一固定在水平面上的物块.今让一小球自左侧槽口A的正上方从静止开始落下,与圆弧槽相切自A点进入槽内,则以下结论中正确的是( )| A. | 小球在半圆槽内运动的全过程中,只有重力对它做功 | |
| B. | 小球在半圆槽内运动的全过程中,小球与半圆槽在水平方向动量守恒 | |
| C. | 小球自半圆槽的最低点B向C点运动的过程中,小球与半圆槽在水平方向动量守 | |
| D. | 若小球从A点静止释放,则小球不能到达C点 |
| A. | 地球表面有两处具有相同的线速度 | |
| B. | 地球表面各处具有相同的角速度 | |
| C. | 地球表面各处具有相同的向心加速度 | |
| D. | 地球表面各处的向心加速度方向都指向地球球心 |
| A. | 只要磁场发生变化就一定产生电磁波 | |
| B. | 任意两列波叠加一定发生干涉现象 | |
| C. | 有振动就一定有波动,有波动就一定有振动 | |
| D. | 脉冲雷达采用的是微波 |
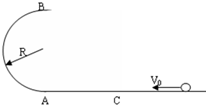 如图所示,半径R=0.4m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.1kg的小球,以初速度v0=7m/s在水平地面上向左作加速度a=3m/s2的匀减速直线运动,运动4.0m后,冲上竖直半圆环,最后小球落在C点.求:
如图所示,半径R=0.4m的光滑半圆环轨道处于竖直平面内,半圆环与粗糙的水平地面相切于圆环的端点A.一质量m=0.1kg的小球,以初速度v0=7m/s在水平地面上向左作加速度a=3m/s2的匀减速直线运动,运动4.0m后,冲上竖直半圆环,最后小球落在C点.求: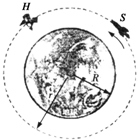 一组宇航员乘坐太空穿梭机S,去修理位于离地球表面h=6.0×105m的圆形轨道上的太空望远镜H.机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,望远镜在穿梭机前方数千米处,如图所示.已知地球半径为R=6.4×106m,地球表面重力加速度为g=9.8m/s2,第一宇宙速度为v=7.9km/s.
一组宇航员乘坐太空穿梭机S,去修理位于离地球表面h=6.0×105m的圆形轨道上的太空望远镜H.机组人员使穿梭机S进入与H相同的轨道并关闭助推火箭,望远镜在穿梭机前方数千米处,如图所示.已知地球半径为R=6.4×106m,地球表面重力加速度为g=9.8m/s2,第一宇宙速度为v=7.9km/s.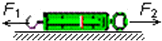 如图示,一个准确的弹簧秤,置于粗糙的水平地面上,用F1=5N的水平力拉秤钩,用F2=6N的水平力拉另一端的圆环,弹簧秤处于静止状态.这时弹簧秤受到的静摩擦力大小是1N,方向水平向左.弹簧秤的示数为5N.
如图示,一个准确的弹簧秤,置于粗糙的水平地面上,用F1=5N的水平力拉秤钩,用F2=6N的水平力拉另一端的圆环,弹簧秤处于静止状态.这时弹簧秤受到的静摩擦力大小是1N,方向水平向左.弹簧秤的示数为5N.