题目内容
如图（甲）所示，两个平行金属板P、Q正对竖直放置，两板间加上如图（乙）所示的交变电压．t=0时，Q板比P板电势高U0，在两板的正中央M点有一电子在电场力作用下由静止开始运动（电子所受重力可忽略不计，电子质量和电荷量分别为m、e ），为使电子不能打在极板上，两极板间的距离至少是多少？分析：平行板电容器两极板带电后形成匀强电场，带电离子在电场中受到力的作用，根据牛顿第二定律求出加速度，根据运动学基本公式分析即可求解．
解答：解：在0＜t＜t0时间内，Q板比P板电势高，E=
，方向水平向左，所以电子所受电场力方向向右，
加速度方向也向右，所以电子向右做匀加速直线运动；
在t0＜t＜2t0时间内，Q板比P板电势低，电场强度方向水平向右，所以电子所受电场力方向向左，加速度方向也向左，所以电子向右做匀减速直线运动，当t=2t0时速度为零；
之后，电子反向加速、再减速，t=4t 0时刻速度再次为0，只有这样，电子才不会打到极板上．
极板间的电场强度：E=
，电子的加速度：
a=
=
t 0时间内的位移：x=
a
=
?
根据运动的对称性，电子减速的位移与加速的位移大小相等．
所以极板之间的最小距离：L=2×2x=
．
答：两极板间的距离至少是L=
．
| U0 |
| d |
加速度方向也向右，所以电子向右做匀加速直线运动；
在t0＜t＜2t0时间内，Q板比P板电势低，电场强度方向水平向右，所以电子所受电场力方向向左，加速度方向也向左，所以电子向右做匀减速直线运动，当t=2t0时速度为零；
之后，电子反向加速、再减速，t=4t 0时刻速度再次为0，只有这样，电子才不会打到极板上．
极板间的电场强度：E=
| U0 |
| d |
a=
| eE |
| m |
| eU0 |
| md |
t 0时间内的位移：x=
| 1 |
| 2 |
| t | 2 0 |
| eU0 |
| md |
| t | 2 0 |
根据运动的对称性，电子减速的位移与加速的位移大小相等．
所以极板之间的最小距离：L=2×2x=
4eU0
| ||
| md |
答：两极板间的距离至少是L=
4eU0
| ||
| md |
点评：本题也可以画出电子运动的速度时间图象求解，难度适中．
练习册系列答案
名校课堂系列答案
相关题目
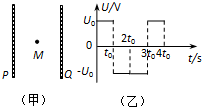如图（甲）所示，两个平行金属板P、Q正对竖直放置，两板间加上如图（乙）所示的交变电压．t=0时，Q板比P板电势高U0，在两板的正中央M点有一电子在电场力作用下由静止开始运动（电子所受重力可忽略不计），已知电子在0～4t0时间内未与两板相碰．则电子速度方向向左且速度大小逐渐增大的时间是（ ）
如图（甲）所示，两个平行金属板P、Q正对竖直放置，两板间加上如图（乙）所示的交变电压．t=0时，Q板的电势比P板高U0，在两板的正中央M点有一质子在电场力作用下由静止开始运动（质子所受重力可忽略不计），已知质子在0～4t0时间内未与两板相碰．则质子速度方向向左且速度大小逐渐减小的时间是（ ）