题目内容
如图(甲)所示,两平行金属板的板长l=已知带电粒子的比荷![]() =
=

(甲) (乙)
(1)在电压u变化的一个周期内,带电粒子能从电场射出的时间。
(2)荧光屏上的发光范围。
(1)带电粒子进入电场后l=v0t①
y=![]()
![]() t2②
t2②
当y=![]() d时,粒子恰能从电场边缘射出,设此时电压为U0
d时,粒子恰能从电场边缘射出,设此时电压为U0
U0=![]() ③
③
U0=900 V 当U>U0时,不能再从电场中射出。粒子能穿出电场的时间为Δt。![]() ④
④
Δt=1.8×10-2 s。⑤
(2)U=0时通过电场的带电粒子从O′点进入磁场向P侧偏转,其所能到达的位置为发生范围的最上端。
qv0B=m![]() ⑥
⑥
R1=
粒子到达PQ上距O″点的距离。
y1=R1-![]() ⑦
⑦
y1=(0.4-![]() ) m=
) m=
当U=U0时,从电场射出的粒子速度最大,与OO′夹角也最大,所以在PQ上向下偏
折最大,其所到达的位置应为发光范围的最下端。
带电粒子离开电场时平行电场线方向速度vy=![]()
离开电场时速度v=![]() ⑨
⑨
偏转角度
tanθ=![]() =
=![]() θ=37°⑩
θ=37°⑩
R2=![]()
![]()
R2=
由几何知识可知,带电粒子的圆心恰好在PQ上,故打到荧光屏上的位置与O″的距离
y2=![]() +R2(1-cos37°)
+R2(1-cos37°) ![]()
y2=![]()
故荧光屏上的发光长度
L′=y1+y2![]()
L′=

练习册系列答案
相关题目
 在“探究平抛运动的规律”的实验中,分成两步进行:
在“探究平抛运动的规律”的实验中,分成两步进行:
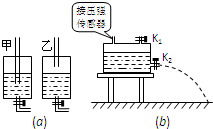 如图(a)所示,两个相同的盛水容器,密闭时装有相同水位的水.现在它们顶部各插有一根两端开口的玻璃管,甲容器中的玻璃管下端插入水中,乙容器中的玻璃管下端在水面上方.若打开容器底部的阀门,两个容器中均有水流出,在开始的一段时间内,水流出的速度不变的是
如图(a)所示,两个相同的盛水容器,密闭时装有相同水位的水.现在它们顶部各插有一根两端开口的玻璃管,甲容器中的玻璃管下端插入水中,乙容器中的玻璃管下端在水面上方.若打开容器底部的阀门,两个容器中均有水流出,在开始的一段时间内,水流出的速度不变的是