Question

如图8-4-10所示，小车静止在光滑水平面上，两个质量相等的人A和B分别站在车的两端.A向前跳后B再向后跳，且两人跳离车时对地的速率相等.则下列说法中正确的是（    ）

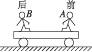
图8-4-10

A.两人跳车后，车向后以一定速度运动，A、B受到的冲量一样大

B.两人跳车后，车向前以一定速度运动，A、B受到的冲量一样大

C.两人跳车后，车速为零，B受到的冲量大些

D.两人跳车后，车速为零，A受到的冲量大些

Answer 1

D

解析:

选地作参考系，取向前方向为正方向，以两人和车的整体为对象，设人、车质量分别为m和M，人跳离车时对地速率为v₀，由动量守恒定律：mv₀-mv₀+Mv=0

得v=0，即车最终静止.

再以A和车为研究对象：

mv₀+(M+m)v₁=0

得到v₁=-v₀

于是对A，由动量定理得：I_A=Δp_A=mv₀-0=mv₀

    对B:I_B=Δp_B=-mv₀-mv₁=-mv₀+v₀=-v₀

     比较得到I_A>｜I_B｜.