题目内容
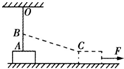 如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中
如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中
- A.地面对物块的支持力FN逐渐增大
- B.地面对物块的摩擦力Ff保持不变
- C.地面对物块的支持力FN逐渐减小
- D.水平拉力F逐渐增大
BD
分析:对A物体进行受力分析,因为A做缓慢直线运动,每一个位置都可以看成平衡状态,运用正交分解法求出支持力的大小,以及拉力的大小.
解答: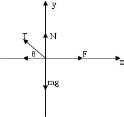 解:物体A受到重力、支持力、水平拉力、弹性绳的拉力和摩擦力.如图.设A处于初始位置时,与B点的距离为h,根据正交分解得:N=mg-kxsinθ=mg-kx
解:物体A受到重力、支持力、水平拉力、弹性绳的拉力和摩擦力.如图.设A处于初始位置时,与B点的距离为h,根据正交分解得:N=mg-kxsinθ=mg-kx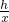 =mg-kh.所以支持力不变,摩擦力f=μN,知地面对A的摩擦力保持不变.F=Tcosθ+f,物块向右运动的过程中,T变大,θ变小,所以F变大.故B、D正确,A、C错误.
=mg-kh.所以支持力不变,摩擦力f=μN,知地面对A的摩擦力保持不变.F=Tcosθ+f,物块向右运动的过程中,T变大,θ变小,所以F变大.故B、D正确,A、C错误.
故选BD.
点评:解决本题的关键能够正确地进行受力分析,熟练运用正交分解去求解力.
分析:对A物体进行受力分析,因为A做缓慢直线运动,每一个位置都可以看成平衡状态,运用正交分解法求出支持力的大小,以及拉力的大小.
解答:
 解:物体A受到重力、支持力、水平拉力、弹性绳的拉力和摩擦力.如图.设A处于初始位置时,与B点的距离为h,根据正交分解得:N=mg-kxsinθ=mg-kx
解:物体A受到重力、支持力、水平拉力、弹性绳的拉力和摩擦力.如图.设A处于初始位置时,与B点的距离为h,根据正交分解得:N=mg-kxsinθ=mg-kx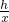 =mg-kh.所以支持力不变,摩擦力f=μN,知地面对A的摩擦力保持不变.F=Tcosθ+f,物块向右运动的过程中,T变大,θ变小,所以F变大.故B、D正确,A、C错误.
=mg-kh.所以支持力不变,摩擦力f=μN,知地面对A的摩擦力保持不变.F=Tcosθ+f,物块向右运动的过程中,T变大,θ变小,所以F变大.故B、D正确,A、C错误.故选BD.
点评:解决本题的关键能够正确地进行受力分析,熟练运用正交分解去求解力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
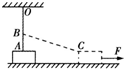 如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中( )
如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中( )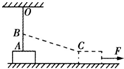
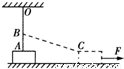 如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中( )
如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中( )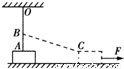 如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中( )
如图所示OA为遵从胡克定律的弹性轻绳,其一端固定于天花板上的0点,另一端与静止在水平地面上的物块m相连,当绳处于竖直位置时,物块m对地面有压力作用,B为紧挨绳的一光滑水平小钉,它到天花板的距离OB等于弹性绳的自然长度.现用一水平力F作用于物块m,使m向右缓慢沿直线运动,物块与地面间有摩擦,则在物块运动过程中( )