��Ŀ����
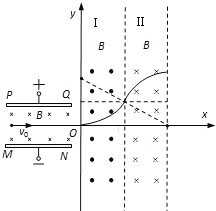
����Ŀ����ͼ��ʾ������ƽ�н�����PQ��MN֮��ľ���Ϊd����������֮���д�ֱֽ���������ǿ�ų����Ÿ�Ӧǿ�ȴ�СΪB����ͼ��������ϵ��x��ƽ���ڽ����壬��������������غϣ�y�ᴹֱ�ڽ�����������I����߽���y�ᣬ�ұ߽�������II����߽��غϣ�����y��ƽ�У�����II�����ұ߽�ƽ����������I������II�ڷֱ������ǿ�ų����Ÿ�Ӧǿ�ȴ�С��ΪB������I�ڵĴų���ֱ��Oxyƽ�����⣬����II�ڵĴų���ֱ��Oxyƽ��������һ��������x���������ٶ�v0����ƽ�а�֮�䣬��ƽ�а��ǡ������x��������ֱ���˶������Ⱥ�ͨ������I��II����֪���ӵ���Ϊe������Ϊm������I������II��x�᷽����Ⱦ�Ϊ![]() �����Ƶ���������
�����Ƶ���������

��1������������֮����Ʋ�U��
��2������Ӵ�����II�ұ߽����ʱ��������������y��
��3����������I�еĴų��������м�����x���������ǿ�糡��ʹ�øõ��Ӹպò��ܴ�����II���ұ߽�ɳ�����������ξ���y���ʱ����t��
���𰸡���1��U=Bv0d����2��![]() ����3��
����3��![]()
��������
�����������1��������ƽ�а����ֱ���˶����糡������������ƽ�⣬
��ƽ�������ã�eE=ev0B����
�糡ǿ�ȣ�E=![]() ����
����
���٢���ʽ������ã�U=Bv0d��
��2������ͼ��ʾ�����ӽ�������I������Բ���˶�������ƫת�����������ṩ��������
��ţ�ٵڶ����ɵã�ev0B=m![]() ����
����
�����������I������y��ƫת����Ϊ y0������I�Ŀ���Ϊb��b=![]() ��
��
����ѧ֪ʶ�ã���R��y0��2+b2=R2 ����
���ۢ�ʽ������ã�y0=![]()
���ݶԳ��ԣ������������ų�������ͬ��ƫת�����ʵ��Ӵ�����II������������Ϊ��
y=2y0=![]()
��3�����Ӹպò��ܴ�����II���ұ߽�ɳ���˵������������II��������Բ���˶��Ĺ켣ǡ��������II���ұ߽����У�Բ�뾶ǡ��������II������ͬ������ӽ�������IIʱ���ٶ�Ϊv��
��ţ�ٵڶ����ɵã�evB=m![]() ����
����
����r=b�ã�v=![]()
����ͨ������I�Ĺ����У��������ȱ���ֱ���˶����˹�����ƽ���ٶ�Ϊ��![]() =
=![]()
����ͨ������I��ʱ�䣺
t1=![]() ��bΪ����I�Ŀ���
��bΪ����I�Ŀ���![]() ������
������
��ã�t1=2��2![]() ��3��
��3��![]()
����������II���˶��˰��Բ�ܣ��������Բ���˶�������ΪT��
��ţ�ٵڶ����ɵã�evB=m![]() ����
����
![]() ����
����
����������II���˶���ʱ�䣺t2=![]() =
=![]() ����
����
���ߢ��ʽ��ã�t2=![]()
���ӷ���ͨ������I��ʱ����Ϊt1���������ξ���y���ʱ������
t=2t1+t2=��8![]() ��12+����
��12+����![]()


