题目内容
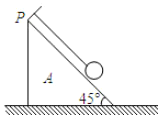
【题目】如图所示,AB是半径为R的四分之一圆弧轨道,轨道底端B点与一水平轨道BC相切,水平轨道又在C点与足够长的斜面轨道CD平滑连接,轨道B处有一挡板(厚度不计)。在圆弧轨道上静止摆放着N个半径为r(r<<R)的光滑刚性小球,恰好将AB轨道铺满,小球从A到B依次标记为1、2、3、…、N号。现将B处挡板抽走,N个小球均开始运动,不计一切摩擦,考虑小球从AB向CD的运动过程,下列说法正确的是( )

A.N个小球在离开圆弧轨道的过程中均作匀速圆周运动
B.1号小球第一次经过B点的速度一定小于![]()
C.1号小球第一次经过B点的向心加速度一定等于2g
D.1号小球第一次沿CD斜面上升的最大高度为R
【答案】B
【解析】
A.受力分析可知,在下滑的过程中,曲面上的小球要做加速运动,故A错误;
B.若第1个小球只有重力对其做功,则在运动到最低点的过程中,根据机械能守恒定律得
![]()
解得
![]()
但是,在第1个球在下滑过程中,始终受到第二个球对它的弹力,该弹力对它做负功,所以第1个小球到达最低点的速度
![]()
故B正确;
C.1号小球第一次经过B点的向心加速度
![]()
所以
![]()
故C错误;
D.1号小球从AB向CD的运动过程中,初始高度为R,如果把N个小球看成整体,则小球运动过程中只有重力做功机械能守恒,弧AB的长度等于小球全部到斜面上的长度,而在园弧上的重心位置小于![]() ,故第N个小球在斜面上能达到的最大高度小于R,1号小球更不能达到R的高度,故D错误。
,故第N个小球在斜面上能达到的最大高度小于R,1号小球更不能达到R的高度,故D错误。
故选B。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目