题目内容
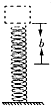 如图所示,一轻质弹簧竖直的固定在水平地面上.将一个质量为m的物块P轻轻的放到弹簧上,当弹簧被压缩了L时(在弹性限度内)物块刚好速度为零.若换一个质量为3m的物块Q轻轻的放到弹簧上,求当弹簧也被压缩L时,求:
如图所示,一轻质弹簧竖直的固定在水平地面上.将一个质量为m的物块P轻轻的放到弹簧上,当弹簧被压缩了L时(在弹性限度内)物块刚好速度为零.若换一个质量为3m的物块Q轻轻的放到弹簧上,求当弹簧也被压缩L时,求:(1)物块Q的加速度.
(2)物块Q的速度.
分析:(1)物块刚好速度为零,说明运动到最低点,而平衡位置为
处,此处重力等于弹力,设弹簧的劲度系数为k,根据平衡条件列式,设物块Q放在弹簧上且弹簧上且弹簧被压缩了L时加速度为a,根据牛顿第二定律列式,联立方程即可求解;
(2)设此时物块Q的速度为v弹簧的弹性势能为E,根据动能定理列式,而根据题意可知,弹簧在压缩L时的弹性势能为E=mgL,联立即可求解.
| L |
| 2 |
(2)设此时物块Q的速度为v弹簧的弹性势能为E,根据动能定理列式,而根据题意可知,弹簧在压缩L时的弹性势能为E=mgL,联立即可求解.
解答:解:(1)设弹簧的劲度系数为k,对物块P有
mg=
kL ①
设物块Q放在弹簧上且弹簧上且弹簧被压缩了L时加速度为a,则有
3mg-kL=3ma ②
由①②式,得
a=
,方向向下
(2)设此时物块Q的速度为v弹簧的弹性势能为E,得
3mgL-E=
(3m)v2
而依题意有E=mgL
∴v=
答:(1)物块Q的加速度的大小为
,方向向下.
(2)物块Q的速度为
.
mg=
| 1 |
| 2 |
设物块Q放在弹簧上且弹簧上且弹簧被压缩了L时加速度为a,则有
3mg-kL=3ma ②
由①②式,得
a=
| g |
| 3 |
(2)设此时物块Q的速度为v弹簧的弹性势能为E,得
3mgL-E=
| 1 |
| 2 |
而依题意有E=mgL
∴v=
|
答:(1)物块Q的加速度的大小为
| g |
| 3 |
(2)物块Q的速度为
|
点评:本题主要考查了动能定理、牛顿第二定律的直接应用,难度适中.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( )
如图所示,一轻质弹簧竖直放置,下端固定在水平面上,上端处于a位置.当一重球放在弹簧上端静止时,弹簧上端被压缩到b位置.现将重球(视为质点)轻放在弹簧a处,由静止释放后,球沿弹簧中轴线向下运动到最低点c处的过程中,下列说法正确的是( ) 如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( )
如图所示,一轻质弹簧与质量为m的物体组成弹簧振子,物体在同一条竖直线上的A、B间做简谐运动,O为平衡位置,C为AO的中点,已知OC=h,振子的周期为T.某时刻物体恰好经过C点并向上运动,则从此时刻开始的半个周期时间内,下列判断正确的是( ) 如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )
如图所示,一轻质弹簧固定在水平地面上,O点为弹簧原长时上端的位置,一个质量为m的物体从O点正上方的A点由静止释放落到弹簧上,物体压缩弹簧到最低点B 后向上运动.则以下说法正确的是( )