题目内容
13.在“用双缝干涉测量光的波长”实验中(1)以下哪些操作能够增大屏上相邻两条亮纹之间的距离?AD
A.将绿色滤光片换为红色滤光片
B.增大双缝之间的距离
C.增大单缝与双缝之间的距离
D.增大双缝与屏之间的距离
(2)转动测量头的手轮,使分划板中心刻线对准第1条亮纹中心,对应的读数是x1=2.190mm,继续转动手轮,使分划板中心刻线对准第5条亮纹中心,对应的读数是x2=7.870mm.则相邻两条亮纹之间的距离是1.420mm.
(3)已知双缝间距d=0.2mm,双缝到屏的距离L=1m.则所测光的波长λ=284nm.
分析 (1)根据双缝干涉条纹的间距公式,判断影响条纹间距的因素.
(2)根据$△x=\frac{{x}_{2}-{x}_{1}}{n}$求出相邻条纹的间距.
(3)根据双缝干涉条纹的间距公式,结合双缝间距、双缝到屏的距离以及相邻条纹的间距,求出波长的大小.
解答 解:(1)A、根据$△x=\frac{L}{d}λ$得,将绿色滤光片换为红色滤光片,波长变大,则相邻条纹间的间距变大.故A正确.
B、根据$△x=\frac{L}{d}λ$得,增大双缝之间的距离,相邻条纹间距变小.故B错误.
C、根据$△x=\frac{L}{d}λ$得,增大单缝和双缝之间的距离,相邻条纹间距不变.故C错误.
D、根据$△x=\frac{L}{d}λ$得,增大双缝与屏之间的距离,则相邻条纹间距变大.故D正确.
故选:AD.
(2)相邻两条亮纹之间的距离:$△x=\frac{{x}_{2}-{x}_{1}}{4}=\frac{7.870-2.190}{4}=1.420mm$.
(3)根据$△x=\frac{L}{d}λ$得:$λ=\frac{△xd}{L}=\frac{1.420×1{0}^{-3}×0.2×1{0}^{-3}}{1}$=2.84×10-7m=284nm.
故答案为:(1)AD;(2)1.420;(3)284.
点评 解决本题的关键掌握双缝干涉条纹的间距公式$△x=\frac{L}{d}λ$,知道影响相邻条纹间距的因素.基础题.

练习册系列答案
相关题目
18.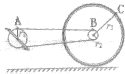 如图所示,自行车的大齿轮与小齿轮通过链条连接,而后轮与小齿轮绕共同轴转动.设大齿轮、小齿轮和后轮的半径分别为r1、r2、r3,在它们的边缘分别取一点A、B、C,设A点的线速度大小为v,则下列关系正确的是( )
如图所示,自行车的大齿轮与小齿轮通过链条连接,而后轮与小齿轮绕共同轴转动.设大齿轮、小齿轮和后轮的半径分别为r1、r2、r3,在它们的边缘分别取一点A、B、C,设A点的线速度大小为v,则下列关系正确的是( )
 如图所示,自行车的大齿轮与小齿轮通过链条连接,而后轮与小齿轮绕共同轴转动.设大齿轮、小齿轮和后轮的半径分别为r1、r2、r3,在它们的边缘分别取一点A、B、C,设A点的线速度大小为v,则下列关系正确的是( )
如图所示,自行车的大齿轮与小齿轮通过链条连接,而后轮与小齿轮绕共同轴转动.设大齿轮、小齿轮和后轮的半径分别为r1、r2、r3,在它们的边缘分别取一点A、B、C,设A点的线速度大小为v,则下列关系正确的是( )| A. | B点的线速度大小为$\frac{{r}_{2}}{{r}_{1}}$v | B. | C点的线速度大小为$\frac{{r}_{3}}{{r}_{2}}$v | ||
| C. | B点的角速度大小为$\frac{v}{{r}_{1}}$ | D. | C点的角速度大小为$\frac{v}{{r}_{3}}$ |
 在垂直纸面向外、磁感应强度为B=1T的匀强磁场中,建立如图所示的竖直直角坐标系xOy,在x<0的区域内有沿x轴负向的匀强电场,场强大小为E=$\sqrt{3}$V/m,在x>0的区域也存在匀强电场(图中未画出).一个带正电油滴从x轴上的N点竖直向下做匀速圆周运动至P点后进入x<0的区域,沿着与水平方向成α=30°角斜向上做直线运动,通过x轴上的M点,已知重力加速度为g=10m/s2,求:
在垂直纸面向外、磁感应强度为B=1T的匀强磁场中,建立如图所示的竖直直角坐标系xOy,在x<0的区域内有沿x轴负向的匀强电场,场强大小为E=$\sqrt{3}$V/m,在x>0的区域也存在匀强电场(图中未画出).一个带正电油滴从x轴上的N点竖直向下做匀速圆周运动至P点后进入x<0的区域,沿着与水平方向成α=30°角斜向上做直线运动,通过x轴上的M点,已知重力加速度为g=10m/s2,求: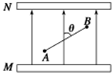 如图所示,MN板间存在匀强电场,场强E=300N/C,方向竖直向上.电场上A、B两点相距10cm,AB连线与电场方向夹角θ=60°,A点和M板相距2cm.求:
如图所示,MN板间存在匀强电场,场强E=300N/C,方向竖直向上.电场上A、B两点相距10cm,AB连线与电场方向夹角θ=60°,A点和M板相距2cm.求: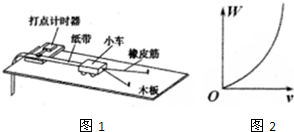 某实验小组采用如图1所示的装置探究功与速度变化的关系,小车在橡皮筋的作用下弹出后,沿木板滑行.打点计时器的工作频率为50Hz.
某实验小组采用如图1所示的装置探究功与速度变化的关系,小车在橡皮筋的作用下弹出后,沿木板滑行.打点计时器的工作频率为50Hz.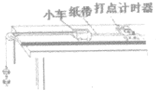 小明把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引力下运动,以此研究绳拉力做功和小车动能变化的关系.此外他还准备了打点计时器及配套电源、导线、复写纸、纸带、小木块、天平(包括砝码)等,实验装置如图
小明把附有滑轮的长木板放在实验桌上,将细绳一端拴在小车上,另一端绕过定滑轮,挂上适当的钩码,使小车在钩码的牵引力下运动,以此研究绳拉力做功和小车动能变化的关系.此外他还准备了打点计时器及配套电源、导线、复写纸、纸带、小木块、天平(包括砝码)等,实验装置如图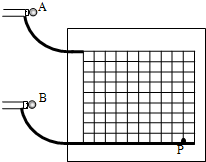 如图所示,在竖直板上不同高度处各固定两个完全相同的圆弧轨道,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断开开关,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一个光滑的水平轨道,则:
如图所示,在竖直板上不同高度处各固定两个完全相同的圆弧轨道,轨道的末端水平,在它们相同位置上各安装一个电磁铁,两个电磁铁由同一个开关控制,通电后,两电磁铁分别吸住相同小铁球A、B,断开开关,两个小球同时开始运动.离开圆弧轨道后,A球做平抛运动,B球进入一个光滑的水平轨道,则: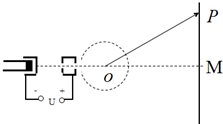 电视机显像管中,电子束的偏转是用磁偏转技术实现.电子束经过电压为U的加速电场后,进入圆形的匀强磁场区,如图12所示,磁场方向垂直于圆面,磁场区的中心为O,半径为r,当不加磁场时,电子束将通过O点而打到屏幕的中心M点.在圆形区域内加垂直圆面、磁感应强度为B的匀强磁场后,电子将打到光屏的上端P点.已知OM=4r,电子的电荷量e,质量为m,不计电子从阴极放出的速度大小,不计空气阻力.求:
电视机显像管中,电子束的偏转是用磁偏转技术实现.电子束经过电压为U的加速电场后,进入圆形的匀强磁场区,如图12所示,磁场方向垂直于圆面,磁场区的中心为O,半径为r,当不加磁场时,电子束将通过O点而打到屏幕的中心M点.在圆形区域内加垂直圆面、磁感应强度为B的匀强磁场后,电子将打到光屏的上端P点.已知OM=4r,电子的电荷量e,质量为m,不计电子从阴极放出的速度大小,不计空气阻力.求: