题目内容
如图所示，点光源S到平面镜M的距离为d．光屏AB与平面镜的初始位置平行．当平面镜M绕垂直于纸面过中心O的转轴以ω的角速度逆时针匀速转过300时，垂直射向平面镜的光线SO在光屏上的光斑P的即时速度大小为8ωd
8ωd
．分析：当平面镜转动θ=30°角时，由光的反射定律可得，反射光线转动2θ角度；根据运动的合成与分解，及圆周运动的角速度与半径的关系，即可求解．
解答：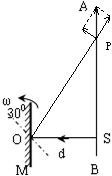
解 设平面镜转过30°角时，光线反射到光屏上的光斑P点，光斑速度为v，由图可知
?v=
，?
而 v⊥=l?2ω=
?2ω，?
故 v=
=8ωd，?
故答案为：8ωd．
解 设平面镜转过30°角时，光线反射到光屏上的光斑P点，光斑速度为v，由图可知?v=
| v⊥ |
| cos2θ |
而 v⊥=l?2ω=
| d |
| cos2θ |
故 v=
| 2ωd |
| cos22θ |
故答案为：8ωd．
点评：考查光的反射定律，掌握运动的合成与分解，理解角速度与半径的关系，并结合几何关系解答．
练习册系列答案
相关题目
