题目内容
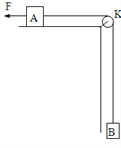
【题目】如图所示,质量M=1 kg的木板静置于倾角θ=37°、足够长的固定光滑斜面底端.质量m=1 kg的小物块(可视为质点)以初速度v0=4 m/s从木板的下端冲上木板,同时在木板上端施加一个沿斜面向上的F=3.2 N的恒力.若小物块恰好不从木板的上端滑下,求木板的长度l为多少?已知小物块与木板之间的动摩擦因数μ=0.8,重力加速度g=10 m/s2,sin 37°=0.6,cos 37°=0.8.

【答案】l=0.5 m
【解析】试题分析:小物块向上匀减速运动,木板向上匀加速运动,当小物块运动到木板的上端时,恰好和木板共速.
设小物块的加速度为![]() ,由牛顿第二定律得,
,由牛顿第二定律得, ![]()
设木板的加速度为![]() ,由牛顿第二定律得,
,由牛顿第二定律得, ![]()
设二者共速的速度为![]() ,经历的时间为
,经历的时间为![]() ,由运动学公式得,
,由运动学公式得, ![]() ,
, ![]()
小物块的位移为![]() ,木板的位移为
,木板的位移为![]() ,由运动学公式得,
,由运动学公式得, ![]()
小物块恰好不从木板上端滑行,有![]() ,联立解
,联立解![]() .
.

练习册系列答案
 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案
相关题目
【题目】某实验小组做“探究弹力和弹簧伸长量的关系”的实验.实验时,先把弹簧平放在桌面上,用刻度尺测出弹簧的原长L0=4.6cm,再把弹簧竖直悬挂起来,在下端挂钩码,每增加一只钩码均记下对应的弹簧的长度x,数据记录如表所示.
钩码个数 | 1 | 2 | 3 | 4 | 5 |
弹力F/N | 1.0 | 2.0 | 3.0 | 4.0 | 5.0 |
弹簧的长度x/cm | 7.0 | 9.0 | 11.0 | 13.0 | 15.0 |
(1)根据表中数据在图中作出F﹣x图线;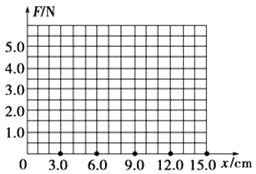
(2)由此图线可得,该弹簧劲度系数k=N/m;
(3)图线与x轴的交点表示 , 其数值大于L0的原因是