题目内容
18.某一人造卫星绕地球做匀速圆周运动,其轨道半径为月球轨道半径的$\frac{1}{3}$,则此卫星运行的周期大约是(d为“天”)( )| A. | 1 d~4 d之间 | B. | 4 d~8 d之间 | C. | 8 d~16 d之间 | D. | 16 d~20 d之间 |
分析 根据万有引力提供向心力,表示出卫星运行的周期,再根据轨道半径的关系求解.
解答 解:万有引力提供向心力,由牛顿第二定律得:G$\frac{Mm}{{r}^{2}}$=m$(\frac{2π}{T})^{2}$r,
解得:T=2π$\sqrt{\frac{{r}^{3}}{GM}}$,
卫星与月球的周期之比:$\frac{{T}_{星}}{{T}_{月}}$=$\sqrt{\frac{1}{27}}$.
月球绕地球运行周期大约为27天,
则卫星的周期为:T星═5.77 天.故B正确,ACD错误.
故选:B.
点评 本题考查了万有引力定律的应用,解决本题的关键掌握万有引力提供向心力这一理论,知道周期与轨道半径的关系.

练习册系列答案
相关题目
9.已知匀变速直线运动的速度公式是V=V0+at 某同学研究匀变速直线运动得到速度与时间关系满足V=3t-2,则他研究的运动的初速度、加速度分别是( )
| A. | 2m/s,3m/s2 | B. | 3m/s,2m/s2 | C. | -2m/s,3m/s2 | D. | -3m/s,2m/s2 |
13.“小小竹排江中游、巍巍青山两岸走”语句中,“巍巍青山两岸走”选取的参考系是( )
| A. | 江中巨石 | B. | 山下树木 | C. | 两岸青山 | D. | 江中竹排 |
3. M、N是一对竖直放置的平行金属板,在两板间加上图示交变电压,位于两板中点P处有一电子,在t=0时速度为零,在t=0.1s时,位于P点右侧s处.设MN间距离足够大,那么在t=0.3s时,电子将位于( )
M、N是一对竖直放置的平行金属板,在两板间加上图示交变电压,位于两板中点P处有一电子,在t=0时速度为零,在t=0.1s时,位于P点右侧s处.设MN间距离足够大,那么在t=0.3s时,电子将位于( )
 M、N是一对竖直放置的平行金属板,在两板间加上图示交变电压,位于两板中点P处有一电子,在t=0时速度为零,在t=0.1s时,位于P点右侧s处.设MN间距离足够大,那么在t=0.3s时,电子将位于( )
M、N是一对竖直放置的平行金属板,在两板间加上图示交变电压,位于两板中点P处有一电子,在t=0时速度为零,在t=0.1s时,位于P点右侧s处.设MN间距离足够大,那么在t=0.3s时,电子将位于( )| A. | P点 | B. | P点右方s处 | C. | P点左方s处 | D. | P点左方2s处 |
10.关于物体带电,下列说法中正确的是( )
| A. | 物体带电是指,物体上只有正电荷 | |
| B. | 物体带电是指,物体上只有负电荷 | |
| C. | 物体带电后物体上的正电荷数与负电荷数不相等 | |
| D. | 以上说法都不对 |
8.下列说法中正确的有( )
| A. | 交流电电器设备上标明的是电压、电流的最大值 | |
| B. | 电容器上标明的电压是有效值 | |
| C. | 交流电压表和电流表测出的是瞬时值 | |
| D. | 220V交流电的电压有效值是220V |
 作用于同一点的两个力F1、F2,的合力F随F1、F2的夹角变化的情况如图所示,且F1<F2,则F1=30N,F2=40N.
作用于同一点的两个力F1、F2,的合力F随F1、F2的夹角变化的情况如图所示,且F1<F2,则F1=30N,F2=40N.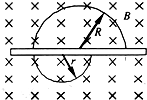 如图所示是带电粒子在匀强磁场中穿透薄片前后的两个半圆弧径迹,径迹半径分别为R和r.带电粒子的质量、电荷量在整个运动过程中均保持不变.问:
如图所示是带电粒子在匀强磁场中穿透薄片前后的两个半圆弧径迹,径迹半径分别为R和r.带电粒子的质量、电荷量在整个运动过程中均保持不变.问: