题目内容
2.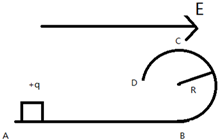 如图所示,一电荷量为+q,质量为m的带电体在A点,AB为动摩擦因数为μ的粗糙平面,优弧BD是半径为R的$\frac{3}{4}$光滑圆道,系统中存在水平向右的匀强电场且Eq=$\frac{3}{4}$mg,重力加速度为g.
如图所示,一电荷量为+q,质量为m的带电体在A点,AB为动摩擦因数为μ的粗糙平面,优弧BD是半径为R的$\frac{3}{4}$光滑圆道,系统中存在水平向右的匀强电场且Eq=$\frac{3}{4}$mg,重力加速度为g.(1)物体可以到达C点时,AB的长度L1;
(2)物体可以到达D点时,AB的长度L2;
(3)在(2)的整个过程中,物体可以达到的Vmax.
分析 (1)物体恰好通过C点时,由重力提供向心力,由向心力公式求出C点的临界速度,再由动能定理求L1.
(2)要使物体可以到达D点时,物体必须能通过速度与电场力和重力的合力相垂直的点P,在P点处,由电场力和重力的合力提供向心力,求该点的速度,再由动能定理求解.
(3)当物体通过P点关于圆心的对称点时速度最大,由动能定理求解.
解答 解: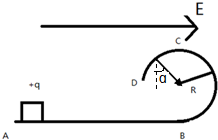 (1)设物体刚好能到达C点时,物体在C点的速度大小是v1;
(1)设物体刚好能到达C点时,物体在C点的速度大小是v1;
则在C点有:mg=m$\frac{{v}_{1}^{2}}{R}$
从A到C,由动能定理得:
qEL1-μmgL1-2mgR=$\frac{1}{2}m{v}_{1}^{2}$
联立解得 L1=$\frac{10R}{3-4μ}$
(2)设物体在CD间的P点时速度方向与电场力和重力的合力垂直,设P点和圆心的连线与竖直方向的夹角为α.
则有 tanα=$\frac{qE}{mg}$=$\frac{3}{4}$,α=37°
在P点有 $\sqrt{(mg)^{2}+(qE)^{2}}$=m$\frac{{v}_{P}^{2}}{R}$
从A到P点,由动能定理得:
qE(L2-Rsinα)-μmgL2-mgR(1+cosα)=$\frac{1}{2}m{v}_{P}^{2}$
解得 L2=$\frac{4.8+\sqrt{2}}{2-2μ}$R
(3)当物体运动到P点关于圆心的对称点Q时速度最大.
从Q到P,由动能定理得:
-2mgRcosα-2qERsinα=$\frac{1}{2}m{v}_{P}^{2}-\frac{1}{2}m{v}_{Q}^{2}$
解得 vQ=$\frac{5}{2}\sqrt{gR}$
故vmax=vQ=$\frac{5}{2}\sqrt{gR}$
答:
(1)物体可以到达C点时,AB的长度L1是$\frac{10R}{3-4μ}$.
(2)物体可以到达D点时,AB的长度L2是$\frac{37R}{30-40μ}$.
(3)在(2)的整个过程中,物体可以达到的vmax是$\frac{5}{2}\sqrt{gR}$.
点评 本题考查带电粒子在电场中的运动,要注意明确解决粒子的运动关键在于明确动能定理和功能关系的正确应用;只要不涉及时间问题,优先考虑功能关系进行分析.

| A. | 1秒很短,所以1秒表示时刻 | |
| B. | 第3秒是指一个时刻 | |
| C. | 12秒80是男子110米栏最新世界纪录,这里的12秒80是指时间 | |
| D. | 物体在5s内指的是物体在4s末到5s末这1s的时间 |
 2012年7月11日上午,中国空军八一飞行表演队、空军跳伞运动大队联袂在西安上演了精彩飞行和跳伞表演.在表演中,八一飞行表演队的6架表演机保持队形,直刺苍穹,做出了18个高难度动作,如图1所示,下列关于飞机运动情况的说法不正确的是( )
2012年7月11日上午,中国空军八一飞行表演队、空军跳伞运动大队联袂在西安上演了精彩飞行和跳伞表演.在表演中,八一飞行表演队的6架表演机保持队形,直刺苍穹,做出了18个高难度动作,如图1所示,下列关于飞机运动情况的说法不正确的是( )| A. | 地面上的人看到飞机飞过,是以地面为参考系 | |
| B. | 飞行员看到观礼台向后掠过,是以飞机为参考系 | |
| C. | 以编队中某一飞机为参考系,其他飞机是运动的 | |
| D. | 以编队中某一飞机为参考系,其他飞机是静止的 |
| A. | 动车组的加速度为0.5 m/s2,接下来的6 s内的位移为78 m | |
| B. | 动车组的加速度为1 m/s2,接下来的6 s内的位移为78 m | |
| C. | 动车组的加速度为0.5 m/s2,接下来的6 s内的位移为96 m | |
| D. | 动车组的加速度为1 m/s2,接下来的6 s内的位移为96 m |
| A. | 在O、A、B三点中,B点电势最低 | |
| B. | 带正电的粒子从B点运动到A点,电场力做正功 | |
| C. | BO间的电势差比OA间的电势差大$\frac{m{{v}_{0}}^{2}}{q}$ | |
| D. | BO间的电势差比OA间的电势差大$\frac{2m{{v}_{0}}^{2}}{q}$ |

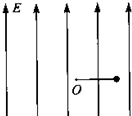 如图所示,空间存在着强度E=$\frac{3mg}{q}$方向竖直向上的匀强电场,在电场内一长为l的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求:
如图所示,空间存在着强度E=$\frac{3mg}{q}$方向竖直向上的匀强电场,在电场内一长为l的绝缘细线,一端固定在O点,一端拴着质量m、电荷量q的小球.现将细线拉直到水平位置,使小球由静止释放,当小球运动最高点时细线受到的拉力恰好达到它能承受的最大值而断裂.求: