题目内容
 2009年10月6日,原香港中文大学校长、“光纤之父”高锟教授获得诺贝尔物理学奖.某有线制导导弹发射时,在导弹发射基地和导弹间连一根细如蛛丝的特制光纤,它双向传输信号,能达到有线制导作用.光纤由纤芯和包层组成,其剖面如图,其中纤芯材料的折射率n1=2,包层折射率n2=
2009年10月6日,原香港中文大学校长、“光纤之父”高锟教授获得诺贝尔物理学奖.某有线制导导弹发射时,在导弹发射基地和导弹间连一根细如蛛丝的特制光纤,它双向传输信号,能达到有线制导作用.光纤由纤芯和包层组成,其剖面如图,其中纤芯材料的折射率n1=2,包层折射率n2=| 3 |
| 3 |
(1)试通过计算说明从光纤一端入射的光信号是否会通过包层“泄漏”出去,
(2)若导弹飞行过程中,将有关参数转变为光信号,利用光纤发回发射基地经瞬间处理后转化为指令光信号返回导弹,求信号往返需要的最长时间.
分析:(1)根据全反射的条件,结合光的折射定律,即可求解;
(2)根据入射角最大时所用的时间最长,及运动的合成与分解,即可求解.
(2)根据入射角最大时所用的时间最长,及运动的合成与分解,即可求解.
解答: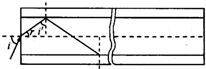 解:(1)如图所示,由题意在纤芯、和包层分界面上全反射临界角C满足
解:(1)如图所示,由题意在纤芯、和包层分界面上全反射临界角C满足
n1sinC=n2sin90°,得C=60°
当在端面上的入射角最大(im=90°)时,折射角r也最大,在纤芯与包层分界面上的入射角i'最小.
在端面上im=90°时,由
n1=
,得rm=30°
这时i'min=90°-30°=60°=C,所以,在所有情况中从端面入射到光纤中的信号都不会从包层中“泄漏”出去.
(2)当在端面上入射角最大时所用的时间最长,这时光在纤芯中总路程为s=
,
光纤中光速v=
,
时间为t=
=
=
s=8×10-5s.
答:(1)通过计算说明从光纤一端入射的光信号不会通过包层“泄漏”出去;
(2)则信号往返需要的最长时间8×10-5s.
 解:(1)如图所示,由题意在纤芯、和包层分界面上全反射临界角C满足
解:(1)如图所示,由题意在纤芯、和包层分界面上全反射临界角C满足n1sinC=n2sin90°,得C=60°
当在端面上的入射角最大(im=90°)时,折射角r也最大,在纤芯与包层分界面上的入射角i'最小.
在端面上im=90°时,由
n1=
| sin90° |
| sinrm |
这时i'min=90°-30°=60°=C,所以,在所有情况中从端面入射到光纤中的信号都不会从包层中“泄漏”出去.
(2)当在端面上入射角最大时所用的时间最长,这时光在纤芯中总路程为s=
| 2L |
| cosrm |
光纤中光速v=
| c |
| n1 |
时间为t=
| s |
| v |
| 2Ln1 |
| c?cosrm |
2×3
| ||
| 3×108×cos30° |
答:(1)通过计算说明从光纤一端入射的光信号不会通过包层“泄漏”出去;
(2)则信号往返需要的最长时间8×10-5s.
点评:考查光的折射定律,掌握全反射的条件,理解运动的合成与分解在其中的应用.

练习册系列答案
相关题目
 2009年10月6日,瑞典皇家科学院在斯德哥尔摩宣布,将2009年诺贝尔物理学奖授予英国华裔科学家高锟以及美国科学家威拉德?博伊尔和乔治?史密斯.高锟在“有关光在纤维中的传输以用于光学通信方面”取得了突破性的成就.光导纤维的结构如图,以下关于光导纤维的说法正确的是( )
2009年10月6日,瑞典皇家科学院在斯德哥尔摩宣布,将2009年诺贝尔物理学奖授予英国华裔科学家高锟以及美国科学家威拉德?博伊尔和乔治?史密斯.高锟在“有关光在纤维中的传输以用于光学通信方面”取得了突破性的成就.光导纤维的结构如图,以下关于光导纤维的说法正确的是( )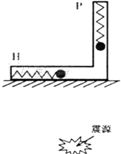 (1)在海地大地震中,设地震波中的横波和纵波传播速率分别约为4km/s和9km/s.如图所示,一种简易地震仪由竖直弹簧振子P和水平弹簧振子H组成,在这次地震中,震源地在地震仪的正下方,若在地面上的观察者观察到两振子的振动相差5s,则
(1)在海地大地震中,设地震波中的横波和纵波传播速率分别约为4km/s和9km/s.如图所示,一种简易地震仪由竖直弹簧振子P和水平弹簧振子H组成,在这次地震中,震源地在地震仪的正下方,若在地面上的观察者观察到两振子的振动相差5s,则