题目内容
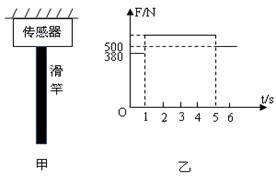
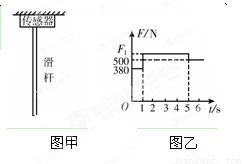
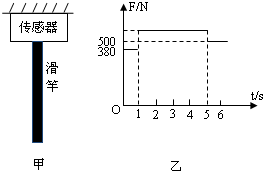 如图甲所示为学校操场上一质量不计的竖直滑竿,滑竿上端固定,下端悬空.为了研究学生沿竿的下滑情况,在竿顶部装有一拉力传感器,可显示竿顶端所受拉力的大小.现有一质量为50kg的学生(可视为质点)从上端由静止开始滑下,5s末滑到竿底时速度恰好为零.以学生开始下滑时刻为计时起点,传感器显示的拉力随时间变化情况如图乙所示,g取10m/s2.
如图甲所示为学校操场上一质量不计的竖直滑竿,滑竿上端固定,下端悬空.为了研究学生沿竿的下滑情况,在竿顶部装有一拉力传感器,可显示竿顶端所受拉力的大小.现有一质量为50kg的学生(可视为质点)从上端由静止开始滑下,5s末滑到竿底时速度恰好为零.以学生开始下滑时刻为计时起点,传感器显示的拉力随时间变化情况如图乙所示,g取10m/s2.
求:
(1)该学生下滑过程中的最大速度;
(2)滑竿的长度.
解:(1)由图读出人的重力G=500N,人的质量为m= .在0-1s内,人的重力大于摩擦力,人做匀加速运动,1-5s内,人的重力小于摩擦力,人做匀减速运动,则在t=1s末人的速度最大.设在0-1s内人的加速度大小分别为a1,根据牛顿第二定律
.在0-1s内,人的重力大于摩擦力,人做匀加速运动,1-5s内,人的重力小于摩擦力,人做匀减速运动,则在t=1s末人的速度最大.设在0-1s内人的加速度大小分别为a1,根据牛顿第二定律
G-F1=ma1
得到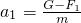 =
=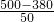 m/s2=2.4m/s2
m/s2=2.4m/s2
t=1s末人的速度最大,最大速度为
vmax=a1t1=2.4×1m/s=2.4m/s
(2)人在0-1s内位移为 =
=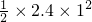 m=1.2m,人在1-5s时间内的位移为
m=1.2m,人在1-5s时间内的位移为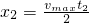 =
=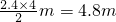
所以滑杆的长度为L=x1+x2=6m
答:
(1)该学生下滑过程中的最大速度为2.4m/s;
(2)滑竿的长度为6m.
分析:(1)滑杆处于静止状态,重力不计,竿顶端所受拉力的大小等于该学生对它的摩擦力大小.由F-t图读出人的重力,求出人的质量,分析人的运动情况.根据牛顿第二定律求出0-1s内人的加速度,再由速度公式求出最大速度.
(2)由位移速度公式求出人匀加速运动和匀减速运动的位移,滑竿的长度等于两段位移大小之和.
点评:本题是已知人的受力情况求解运动情况的问题,也可以通过作速度时间图象分析运动过程,滑杆长度也可以这样求:L=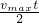 =6m.
=6m.
 .在0-1s内,人的重力大于摩擦力,人做匀加速运动,1-5s内,人的重力小于摩擦力,人做匀减速运动,则在t=1s末人的速度最大.设在0-1s内人的加速度大小分别为a1,根据牛顿第二定律
.在0-1s内,人的重力大于摩擦力,人做匀加速运动,1-5s内,人的重力小于摩擦力,人做匀减速运动,则在t=1s末人的速度最大.设在0-1s内人的加速度大小分别为a1,根据牛顿第二定律G-F1=ma1
得到
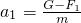 =
=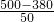 m/s2=2.4m/s2
m/s2=2.4m/s2t=1s末人的速度最大,最大速度为
vmax=a1t1=2.4×1m/s=2.4m/s
(2)人在0-1s内位移为
 =
=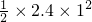 m=1.2m,人在1-5s时间内的位移为
m=1.2m,人在1-5s时间内的位移为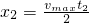 =
=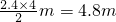
所以滑杆的长度为L=x1+x2=6m
答:
(1)该学生下滑过程中的最大速度为2.4m/s;
(2)滑竿的长度为6m.
分析:(1)滑杆处于静止状态,重力不计,竿顶端所受拉力的大小等于该学生对它的摩擦力大小.由F-t图读出人的重力,求出人的质量,分析人的运动情况.根据牛顿第二定律求出0-1s内人的加速度,再由速度公式求出最大速度.
(2)由位移速度公式求出人匀加速运动和匀减速运动的位移,滑竿的长度等于两段位移大小之和.
点评:本题是已知人的受力情况求解运动情况的问题,也可以通过作速度时间图象分析运动过程,滑杆长度也可以这样求:L=
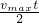 =6m.
=6m. 
练习册系列答案
相关题目
 (2011?江苏模拟)如图甲所示为学校操场上一质量不计的竖直滑竿,滑竿上端固定,下端悬空.为了研究学生沿竿的下滑情况,在竿顶部装有一拉力传感器,可显示竿顶端所受拉力的大小.现有一质量为50kg的学生(可视为质点)从上端由静止开始滑下,5s末滑到竿底时速度恰好为零.以学生开始下滑时刻为计时起点,传感器显示的拉力随时间变化情况如图乙所示,g取10m/s2.
(2011?江苏模拟)如图甲所示为学校操场上一质量不计的竖直滑竿,滑竿上端固定,下端悬空.为了研究学生沿竿的下滑情况,在竿顶部装有一拉力传感器,可显示竿顶端所受拉力的大小.现有一质量为50kg的学生(可视为质点)从上端由静止开始滑下,5s末滑到竿底时速度恰好为零.以学生开始下滑时刻为计时起点,传感器显示的拉力随时间变化情况如图乙所示,g取10m/s2. 如图甲所示为学校操场上一质量不计的竖直滑杆,滑杆上端固定.为了研究学生沿杆的下滑情况,在杆顶部装有一拉力传感器,可显示杆顶部所受力的大小.现有一学生(可视为质点)从上端由静止开始滑下,5s末滑到杆底端时速度恰好为零.以学生开始下滑时刻为计时起点,传感器显示的拉力随时间变化的情况如图乙所示,g取10m/s2.求:
如图甲所示为学校操场上一质量不计的竖直滑杆,滑杆上端固定.为了研究学生沿杆的下滑情况,在杆顶部装有一拉力传感器,可显示杆顶部所受力的大小.现有一学生(可视为质点)从上端由静止开始滑下,5s末滑到杆底端时速度恰好为零.以学生开始下滑时刻为计时起点,传感器显示的拉力随时间变化的情况如图乙所示,g取10m/s2.求: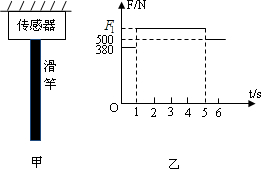 如图甲所示为学校操场上一质量不计的竖直滑杆,滑杆上端固定,下端悬空,为了研究学生沿杆的下滑情况,在竿的顶部装有一拉力传感器,可显示竿顶端所受拉力的大小,现有一学生(可视为质点)从上端由静止开始滑下,5s未滑到竿底时速度恰好为零,从学生开始下滑的时刻计时,传感器显示拉力随时间变化情况如图乙所示,g取10m/s2,求
如图甲所示为学校操场上一质量不计的竖直滑杆,滑杆上端固定,下端悬空,为了研究学生沿杆的下滑情况,在竿的顶部装有一拉力传感器,可显示竿顶端所受拉力的大小,现有一学生(可视为质点)从上端由静止开始滑下,5s未滑到竿底时速度恰好为零,从学生开始下滑的时刻计时,传感器显示拉力随时间变化情况如图乙所示,g取10m/s2,求