Question

【题目】如图甲，质量为1kg的滑块受到一个沿斜面方向的外力F作用，从斜面底端开始，以初速度v0＝3.6m/s沿着倾角为37°足够长的斜面向上运动，物体与斜面间的动摩擦因数为μ＝0.8。滑块开始一段时间内的速度-时间图像如图所示乙（g取10m/s2，sin37°＝0.6，cos37°＝0.8）。求：

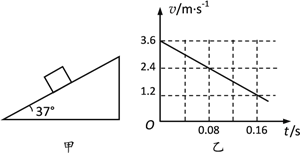
（1）滑块上滑过程中加速度的大小和方向；

（2）滑块所受外力F的大小和方向；

（3）当滑块到最高点时撤除外力，此后滑块能否返回斜面底端？若不能返回，求出滑块停在离斜面底端的距离。若能返回，求出返回斜面底端时的速度。

Answer 1

【答案】(1) ，沿斜面向下 (2) -2.6N，方向平行于斜面向下 (3) 滑块不能返回斜面底端；停在距斜面底端0.43m处

【解析】（1）根据速度-时间图象的斜率表示加速度得：

沿斜面向下；

（2）设F沿斜面向上，则mgsinθ-μmgcosθ-F=ma

F=mgsinθ+μmgcosθ-ma=1×10×0.6+0.8×1×10×0.8-1×15N=-2.6N

所以F力的方向平行于斜面向下．

（3）因为 mgsinθ＜μmgcosθ，所以滑块不能返回斜面底端．

设经过时间t，滑块速度为零，则t= =0.24s

滑块停在距离斜面底端0.43m处．