题目内容
18.人造卫星离地球表面距离等于地球半径R,卫星以速度v沿圆轨道运动,设地面上的重力加速度为g,则( )| A. | v=2$\sqrt{gR}$? | B. | v=$\sqrt{2gR}$? | C. | v=$\sqrt{gR}$? | D. | v=$\sqrt{\frac{gR}{2}}$ |
分析 要求第一宇宙速度可根据G$\frac{Mm}{{R}^{2}}$=$m\frac{{v}^{2}}{R}$和G$\frac{Mm}{{R}^{2}}$=mg求解即可.
解答 解:根据万有引力提供向心力得:G$\frac{Mm}{{R}^{2}}$=$m\frac{{v}^{2}}{R}$
得第一宇宙速度为:v=$\sqrt{\frac{GM}{R}}$
忽略地球的自转对重力加速度的影响,根据万有引力定律得:G$\frac{Mm}{{R}^{2}}$=mg
故有:GM=gR2
则地球的第一宇宙速度为:v=$\sqrt{gR}$.选项C正确,ABD错误.
故选:C
点评 万有引力提供向心力,忽略自转万有引力等于物体在地球表面所受的重力是求第一宇宙速度的基本方法,要注意掌握.当中心天体的质量不知时一定要用黄金代换公式G$\frac{Mm}{{R}^{2}}$=mg,进行代换.

练习册系列答案
 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案
相关题目
8.牛顿从太阳与行星间的引力得出万有引力定律,经历了如下的认识过程:①“月-地检验”;②科学猜想;③演绎推广.以上认识阶段的合理顺序是( )
| A. | ①②③ | B. | ③②① | C. | ②①③ | D. | ②③① |
6.甲、乙两物体在t=0时刻经过同一位置沿x轴运动,其v-t图象如图所示,则( ) 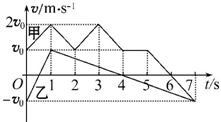

| A. | 甲、乙在t=0到t=1s之间沿同一方向运动 | |
| B. | 乙在t=0到t=7s之间的位移为零 | |
| C. | 在t=4s时甲、乙相距4.5v0 | |
| D. | 甲、乙在t=6s时的加速度方向相同 |
13. 如图所示,A、B是两个摩擦转动的靠背轮,A是主动轮,B是从动轮,它们的半径Ra=2Rb,a和b分别是A和B边缘上一点,c和d在各轮半径的中点,下列判断正确的是( )
如图所示,A、B是两个摩擦转动的靠背轮,A是主动轮,B是从动轮,它们的半径Ra=2Rb,a和b分别是A和B边缘上一点,c和d在各轮半径的中点,下列判断正确的是( )
 如图所示,A、B是两个摩擦转动的靠背轮,A是主动轮,B是从动轮,它们的半径Ra=2Rb,a和b分别是A和B边缘上一点,c和d在各轮半径的中点,下列判断正确的是( )
如图所示,A、B是两个摩擦转动的靠背轮,A是主动轮,B是从动轮,它们的半径Ra=2Rb,a和b分别是A和B边缘上一点,c和d在各轮半径的中点,下列判断正确的是( )| A. | va=$\frac{1}{2}$vc | B. | vc=vd | C. | wb=2wd | D. | wa=2wd |
10.以下关于物理学史的说法正确的是( )
| A. | 电荷量e的数值最早是由法国学者库仑用实验测得的 | |
| B. | “电流的周围存在磁场”最早是由安培发现的 | |
| C. | 牛顿运用理想实验法得出“力不是维持物体运动的原因” | |
| D. | 伽利略通过“小球在斜面上的运动”实验推出了落体运动规律 |
7.下列有关物理知识的说法,正确的是( )
| A. | 一个力作用于物体上,该力一定要对物体做功 | |
| B. | 牛顿的经典力学理论不仅适用于宏观低速运动物体,也适用于微观高速运动物体 | |
| C. | 由万有引力定律可知,两个物体无限接近时,他们的万有引力将无穷大 | |
| D. | 卡文迪许扭秤装置第一次比较准确地测出了引力常量 |
 如图所示,线圈L有足够大的电感,其自身直流电阻为零,L1和L2是两个相同的小灯泡,在下面两种情况下,小灯泡亮度变化情况是:
如图所示,线圈L有足够大的电感,其自身直流电阻为零,L1和L2是两个相同的小灯泡,在下面两种情况下,小灯泡亮度变化情况是: 如图,升降机内有一固定斜面,斜面上放一物体,开始时升降机做匀速运动,物块相对斜面匀速下滑,当升降机加速上升时物块与斜面间的正压力将增大(填增大或减小)
如图,升降机内有一固定斜面,斜面上放一物体,开始时升降机做匀速运动,物块相对斜面匀速下滑,当升降机加速上升时物块与斜面间的正压力将增大(填增大或减小)