题目内容
6. 如图所示,一根长 L=1.5m 的光滑绝缘细直杆MN,竖直固定在场强为 E=1.0×105N/C.与水平方向成θ=30°角的倾斜向上的匀强电场中.杆的下端M固定一个带电小球 A,电荷量Q=+4.5×10-6C;另一带电小球 B 穿在杆上可自由滑动,电荷量q=+1.0×10-6 C,质量m=1.0×10-2 kg.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×10 9N•m2/C2,取 g=l0m/s2)
如图所示,一根长 L=1.5m 的光滑绝缘细直杆MN,竖直固定在场强为 E=1.0×105N/C.与水平方向成θ=30°角的倾斜向上的匀强电场中.杆的下端M固定一个带电小球 A,电荷量Q=+4.5×10-6C;另一带电小球 B 穿在杆上可自由滑动,电荷量q=+1.0×10-6 C,质量m=1.0×10-2 kg.现将小球B从杆的上端N静止释放,小球B开始运动.(静电力常量k=9.0×10 9N•m2/C2,取 g=l0m/s2)(1)小球B开始运动时的加速度为多大?
(2)小球B的速度最大时,距M端的高度h1为多大?
(3)小球B从N端运动到距M端的高度h2=0.61m时,速度为v=1.0m/s,求此过程中小球B的电势能改变了多少?
分析 (1)对小球B进行受力分析,运用牛顿第二定律求出开始运动时的加速度大小.
(2)根据受力情况分析小球B的运动情况.小球B向下运动,受A的斥力增大,加速度减小,速度增大,当小球B速度最大时合力减为零.由平衡条件和库仑定律求解.
(3)由于A对B的库仑力做功是变力功,所以运用动能定理求解电场力做功,即可得到电势能的变化量.
解答 解:(1)开始运动时小球B受重力、库仑力、杆的弹力和电场力,沿杆方向运动,将电场力沿杆的方向和垂直杆的方向分解,由牛顿第二定律得:
mg-$\frac{kQq}{{L}^{2}}$-qEsinθ=ma
解得:a=g-$\frac{kQq}{{L}^{2}m}$
代入数据解得:a=3.2 m/s2.
(2)小球B向下运动,受A的斥力增大,加速度减小,速度增大,当小球B速度最大时合力减为零,即:
$\frac{kQq}{{h}_{1}^{2}}$+qEsinθ=mg
解得:h1=$\sqrt{\frac{kQq}{mg-qEsinθ}}$
代入数据解得:h1=0.9 m.
(3)小球B从开始运动到速度为v的过程中,设重力做功为W1,电场力做功为W2,库仑力做功为W3,根据动能定理有:
W1+W2+W3=$\frac{1}{2}$mv2
W1=mg(L-h2)
W2=-qE(L-h2)sinθ
解得:W3=$\frac{1}{2}$mv2-mg(L-h2)+qE(L-h2)sinθ
从功能角度来说,电势能的改变量的大小就等于电场力做的功.电场力做负功,电势能增大.动能的改变量就等于总功.
设小球B的电势能改变了△Ep,则:△Ep=-(W2+W3)
△Ep=mg(L-h2)-$\frac{1}{2}$mv2
解得:△Ep=8.4×10-2J
答:(1)小球B开始运动时的加速度为3.2 m/s2 ;
(2)小球B的速度最大时,距M端的高度h1为0.9 m;
(3)小此过程中小球B的电势能增加了8.4×10-2J.
点评 此题关键能够正确对小球B进行受力分析和运动分析,知道电场力做功量度电势能的变化,常用动能定理求解变力功.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
| A. | 自由电荷通过了电容器两板间的绝缘电介质 | |
| B. | 自由电荷没有通过电容器两板间的绝缘电介质 | |
| C. | 接入交变电源使电容器两极板间的绝缘电介质变成了导体 | |
| D. | 电容器交替进行充放电,电路中就有电流,表现为交变电流“通过”了电容器 |
| A. | mgH-mgh-W | B. | W+mgH-mgh | C. | mgh+mgH-W | D. | W+mgh-mgH |
| A. | 2F | B. | 4F | C. | $\frac{F}{8}$ | D. | $\frac{F}{4}$ |
 如图,有三个质量相等的小球,一个带正电、一个带负电、一个不带电,从平行板(两板水平放置,电场竖直)的电场中P点以相同的初速度垂直于电场方向进入电场,它们分别落在A.B.C三点.已知该平行板下板带正电,上板带负电.可以判断( )
如图,有三个质量相等的小球,一个带正电、一个带负电、一个不带电,从平行板(两板水平放置,电场竖直)的电场中P点以相同的初速度垂直于电场方向进入电场,它们分别落在A.B.C三点.已知该平行板下板带正电,上板带负电.可以判断( )| A. | 落在A点的小球带正电,落在B点的小球不带电 | |
| B. | 三个小球在电场中运动的时间相等 | |
| C. | 三个小球到达极板时的动能关系为EkA>EkB>EkC | |
| D. | 三个小球在电场中运动时的加速度关系为aA>aB>aC |
| A. |  | B. |  | C. | 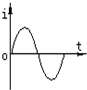 | D. |  |
| A. | 飘落中的秋叶 | B. | 被掷出后在空中运动的铅球 | ||
| C. | 乘电梯匀速上升的人 | D. | 沿粗糙斜面匀速下滑的木箱 |
| A. | 如果入射小球每次都从同一位置由静止滚下,重复几次落点应该是重合的 | |
| B. | 由于偶然因素的存在,重复几次的落点不重合也是正常的,但是落点应比较集中 | |
| C. | 测量P点位置时,如果重复10次的落点分别是P1、P2、P3、…、P10,则OP应是OP1、OP2、OP3、…、OP10的平均值 | |
| D. | 用半径尽量小的圆把P1、P2、P3、…、P10圈住,圆心就是落点平均位置P |