题目内容
质量分别为m
1和m
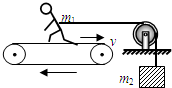
2的两个小物块用轻绳连结,绳跨过位于倾角α=30°的粗糙斜面体顶端的轻滑轮,斜面体固定在水平桌面上,如图所示.已知滑轮与转轴之间的摩擦不计,m
1、m
2与斜面体之间的动摩擦因数为
μ=,且
=.第一次,m
1悬空(未与斜面体接触),m
2放在斜面上,m
2自斜面底端由静止开始运动至斜面顶端所用的时间为t
1;第二次,将m
1和m
2位置互换,使m
2悬空,m
1放在斜面上,则m
1自斜面底端由静止开始运动至斜面顶端所需的时间为t
2.求
=?

由题意可得:m
1与m
2的加速度大小相等.设斜面长为l
第一次,小物块受力情况如图所示,
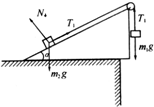
设T
1为绳中张力,a
1为两物块加速度的大小,则有:
m
1g-T
1=m
1a
1 ①
T
1-m
2gsinα-μm
2gcosα=m
2a
1 ②由①和②式可得:
m
1g-m
2gsinα-μm
2gconα=(m
1+m
2)a
1 ③
第二次,m
1与m
2交换位置.设绳中张力为T
2,两物块加速度的大小为a
2,则有:
m
2g-T
2=m
2a
2 ④
T
2-m
1gsinα-μm
1gcosα=m
1a
2⑤
由④和⑤式可得:
m
2g-m
1gsinα-μm
1gcosα=(m
1+m
2)a
2⑥
代入
α=30°,μ=,=可得
==又两次均从斜面底端运动到顶端,所以
l=a1t12=a2t22所以:
===答:
=
练习册系列答案
相关题目