题目内容
15.一个容器中有2g氢气,假设所有氢原子均处于第5能级,在向低能级跃迁时,求:(1)一共能辐射几种光子?
(2)若阿伏加德罗常数用NA表示,当所有氢原子都跃迁到基态时,辐射的光子总数为多少?
分析 本题考查了波尔原子理论:从高轨道向低轨道跃迁时减少的能量以光子的形式辐射出去;所有的激发态都是不稳定的,都会继续向基态跃迁,故辐射光子的种类为${C}_{n}^{2}$,c=λγ,故波长越大,频率越短.
解答 解:(1)处于第5能级的激发态氢原子向低能级跃迁时,
能产生n=${C}_{5}^{2}$=10种;
(2)2g氢气共含有2NA个氢原子
如图所示,处于第5能级时,有4种跃迁方式,每种跃迁方式各放出$\frac{1}{4}$×2NA=$\frac{1}{2}$NA个光子;
处于第4能级的原子数为$\frac{1}{2}$NA,有3种跃迁方式,各放出$\frac{1}{3}$×$\frac{1}{2}$NA=$\frac{1}{6}$NA个光子;
处于第3能级的原子数为$\frac{1}{2}$NA+$\frac{1}{6}$NA=$\frac{2}{3}$NA,有两种跃迁方式,各放出$\frac{1}{2}$×$\frac{2}{3}$NA=$\frac{1}{3}$NA个光子;
处于第2能级的原子数为$\frac{1}{2}$NA+$\frac{1}{6}$NA+$\frac{1}{3}$NA=NA,只有一种跃迁方式,放出NA个光子;
放出的光子总数为N总=4×$\frac{1}{2}$NA+3×$\frac{1}{6}$NA+2×$\frac{1}{3}$NA+NA=$\frac{25}{6}$NA.
答:(1)一共能辐射10种
(2)若阿伏加德罗常数用NA表示,当所有氢原子都跃迁到基态时,辐射的光子总数为$\frac{25}{6}$NA.
点评 解决本题的关键原子的能量是量子化,能级差也是量子化的,不同的能级跃迁发出的光子频率不同.

练习册系列答案
相关题目
1.光滑水平面上水平放置一弹簧AB,A端固定,B端受到1N的拉力时弹簧伸长5cm.现在在B点系一个质量为100g的小球,并使弹簧伸长10cm,放手后让其做简谐运动.它的振幅是和振动中加速度的最大值各是( )
| A. | 5cm 10m/s2 | B. | 10cm 20m/s2 | C. | 5cm 5m/s2 | D. | 10cm 5m/s2 |
2.在“研究平抛物体运动”实验中,如果小球每次从斜槽滚下的初始位置不同,则下列说法中正确的是( )
| A. | 小球平抛的初速度不同 | B. | 小球通过的水平位移相同 | ||
| C. | 小球在空中运动的时间不同 | D. | 小球每次做不同的抛物线运动 |
3.带电量分别为2Q、4Q的两点电荷,相距为r,相互作用力为F.现把两个电荷的电量各减少一半,距离减小为$\frac{r}{4}$,则两个点电荷的相互作用力变为( )
| A. | 4F | B. | 2F | C. | $\frac{F}{2}$ | D. | $\frac{F}{4}$ |
10.如图用插针法测定玻璃的折射率的实验中,以下说法正确的是 ( )
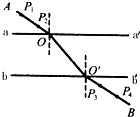

| A. | P1、P2及P3、P4之间的距离适当大一些,可以减小误差 | |
| B. | 入射角不能太大,因为折射光线会在玻璃砖的内表面发生全发射,使实验无法进行 | |
| C. | 玻璃砖的宽度宜大些 | |
| D. | 可以直接用铅笔沿玻璃砖边缘画出边界aa,和bb |
20.存在下列事实:
①一对高能的γ光子相遇时可能产生一对正负电子;
②一个孤立的γ光子不论其频率多高都不可能产生一对正负电子;
③一个高能的γ光子经过重核附近时可能产生一对正负电子;
④原子核发生变化时,只发射一些特定频率的γ光子.
关于上述事实下列说法正确的是(电子质量me,光在真空中速度为c,普朗克常量为h)( )
①一对高能的γ光子相遇时可能产生一对正负电子;
②一个孤立的γ光子不论其频率多高都不可能产生一对正负电子;
③一个高能的γ光子经过重核附近时可能产生一对正负电子;
④原子核发生变化时,只发射一些特定频率的γ光子.
关于上述事实下列说法正确的是(电子质量me,光在真空中速度为c,普朗克常量为h)( )
| A. | 事实①表明,微观世界中的相互作用,只要符合能量守恒的事件就一定能发生 | |
| B. | 事实②说明,动量守恒定律和能量守恒定律是自然界的普遍规律 | |
| C. | 事实③中,由于外界重核的参与,系统动量不守恒,而γ光子的频率需满足ν≥$\frac{me{c}^{2}}{h}$ | |
| D. | 事实④中表明,原子核的能级也是不连续的 |
4.一个自由摆动的秋千,摆动的幅度越来越小,下列说法中正确的是( )
| A. | 机械能守恒 | B. | 能量正在消失 | ||
| C. | 机械能正在转化为内能 | D. | 内能正在转化为机械能 |
5. 质点所受的力F随时间t变化的规律如图所示,力的方向始终在一直线上.已知t=0时,质点的速度为零,则下列判断中正确的是( )
质点所受的力F随时间t变化的规律如图所示,力的方向始终在一直线上.已知t=0时,质点的速度为零,则下列判断中正确的是( )
 质点所受的力F随时间t变化的规律如图所示,力的方向始终在一直线上.已知t=0时,质点的速度为零,则下列判断中正确的是( )
质点所受的力F随时间t变化的规律如图所示,力的方向始终在一直线上.已知t=0时,质点的速度为零,则下列判断中正确的是( )| A. | 0、t2、t4时刻质点的加速度最大 | B. | t2时刻质点的动能最大 | ||
| C. | t4时刻质点回到出发点 | D. | 力F始终对物体作正功 |