题目内容
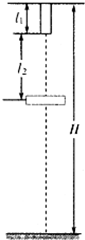 如图所示,长为l1=5m的竖直杆上端距地面H=50m,杆正下方距杆下端l2=12m处有一薄圆环.杆由静止释放,1s后圆环也由静止释放,杆和环均不转动,不计空气阻力,取10g=m/s2,求:
如图所示,长为l1=5m的竖直杆上端距地面H=50m,杆正下方距杆下端l2=12m处有一薄圆环.杆由静止释放,1s后圆环也由静止释放,杆和环均不转动,不计空气阻力,取10g=m/s2,求:(l)杆追上圆环后穿过环所用的时间;
(2)杆穿过圆环后,杆上端与圆环的最大距离.
分析:(1)先根据位移时间关系公式列式求解杆追上环的时间,同理根据位移时间关系公式列式求解杆的上端点追上环的时间,然后求解时间差即可;
(2)杆落地时两者距离最远,先根据位移时间关系公式求解杆落地的时间,然后根据位移时间关系求解环的位移,结合几何关系得到最大间距.
(2)杆落地时两者距离最远,先根据位移时间关系公式求解杆落地的时间,然后根据位移时间关系求解环的位移,结合几何关系得到最大间距.
解答:解:(1)设杆下落后经过时间t1下端追上圆环,有:
g
-l2=
g(t1-1)2
解得:t1=1.7s
设经过时间t2杆上段离开圆环,有:
g
-l1-l2=
g(t2-1)2
解得:t2=2.2s
穿过圆环时间:t=t2-t1=0.5s
(2)杆落地时两者距离最远,设杆经过t3落地,有:H-l1=
g
解得:t3=3s
圆环下降距离:h=
g(t3-1)2=20m
最大距离:△h=(H-l1)-(l1+l2+h)=8m
答:(l)杆追上圆环后穿过环所用的时间为0.5s;(2)杆穿过圆环后,杆上端与圆环的最大距离为8m.
| 1 |
| 2 |
| t | 2 1 |
| 1 |
| 2 |
解得:t1=1.7s
设经过时间t2杆上段离开圆环,有:
| 1 |
| 2 |
| t | 2 2 |
| 1 |
| 2 |
解得:t2=2.2s
穿过圆环时间:t=t2-t1=0.5s
(2)杆落地时两者距离最远,设杆经过t3落地,有:H-l1=
| 1 |
| 2 |
| t | 2 3 |
解得:t3=3s
圆环下降距离:h=
| 1 |
| 2 |
最大距离:△h=(H-l1)-(l1+l2+h)=8m
答:(l)杆追上圆环后穿过环所用的时间为0.5s;(2)杆穿过圆环后,杆上端与圆环的最大距离为8m.
点评:本题关键是明确杆和环的运动规律,然后多次根据位移时间关系公式列式求解,不难.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案
相关题目
 如图所示,长为L1,宽为L2的矩形线圈电阻为R,处于磁感应强度为B的匀强磁场边缘,线圈与磁感线垂直.将线圈以向右的速度v匀速拉出磁场的过程中( )
如图所示,长为L1,宽为L2的矩形线圈电阻为R,处于磁感应强度为B的匀强磁场边缘,线圈与磁感线垂直.将线圈以向右的速度v匀速拉出磁场的过程中( )