��Ŀ����
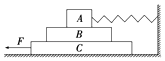
����Ŀ����ͼ��ʾ�������S=40cm2��Բ��������C�������Ϸ�����ˮƽ�����ϣ�����һ�������ƶ��Ļ��������һ���������������壬�����쳤��ϸ��һ��ϵ������Ϊ 2kg�����ϣ���һ�˿��������������������Ϊ10kg������A����ʼʱ���¶�t1=7�棬�������ľ���l1=10cm������A�ĵײ����h1=4cm����֪������ѹp0=1.0��105Pa���䣬�ֶ������ڵ����建������ֱ��A���崥�أ����ʣ����������ٶ�g=l0m/s2��
��1����ʼʱ�����ѹǿΪ����Pa��
��2��������A�մ���ʱ��������¶�Ϊ���١棿
���𰸡�
��1���⣺��������ƽ�⣺P0S+mg=P1S+T��
T=mAg��
���������ѹǿP1=P0�� ![]() =0.8��105Pa
=0.8��105Pa
�𣺿�ʼʱ�����ѹǿΪ0.8��105Pa��
��2���⣺��״̬��V1=l1s��T1=280K
ĩ״̬��V2=��l1+h1��s��T2=��
��ѹ�仯�� ![]() ���������ݣ���T2=392K����t2=119��
���������ݣ���T2=392K����t2=119��
�𣺵�����A�մ���ʱ��������¶�Ϊ119�森
����������1�����ݻ���ƽ�⣬��ʽ��������ѹǿ����2�����ݼ��ι�ϵ�õ�����ı仯�����Ȼ����ݵ�ѹ�仯��ʽ��ʽ��⣮

��ϰ��ϵ�д�
 �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д� С����ȫ�ܼ��ϵ�д�
С����ȫ�ܼ��ϵ�д�
�����Ŀ