题目内容
在绝缘粗糙的水平面上相距为6L的A、B两处分别固定电量不等的正电荷,两电荷的位置坐标如图(甲)所示,已知B处电荷的电量为+Q.图(乙)是AB连线之间的电势φ与位置x之间的关系图象,图中x=L点为图线的最低点,x=-2L处的纵坐标φ=φ0,x=0处的纵坐标φ=
φ0,x=2L处的纵坐标φ=
φ0.若在x=-2L的C点由静止释放一个质量为m、电量为+q的带电物块(可视为质点),物块随即向右运动.求:

(1)固定在A处的电荷的电量QA;
(2)为了使小物块能够到达x=2L处,试讨论小物块与水平面间的动摩擦因数μ所满足的条件;
(3)若小物块与水平面间的动摩擦因数μ=
,小物块运动到何处时速度最大?并求最大速度vm;
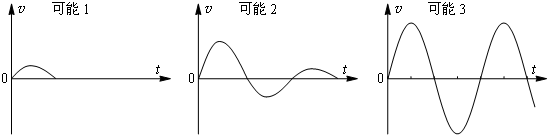
(4)试画出μ取值不同的情况下,物块在AB之间运动大致的速度-时间关系图象.
| 25 |
| 63 |
| 3 |
| 7 |

(1)固定在A处的电荷的电量QA;
(2)为了使小物块能够到达x=2L处,试讨论小物块与水平面间的动摩擦因数μ所满足的条件;
(3)若小物块与水平面间的动摩擦因数μ=
| kqQ |
| 3mgL2 |
(4)试画出μ取值不同的情况下,物块在AB之间运动大致的速度-时间关系图象.
(1)由图(乙)得,x=L点为图线的最低点,切线斜率为零,
即合场强E合=0
所以
=
得
=
解得QA=4Q;
(2)物块先做加速运动再做减速运动,到达x=2L处速度vt≥0
从x=-2L到x=2L过程中,由动能定理得:
qU1-μmgs1=
mv12-0,
即q(φ0-
φ0)-μmg(4L)=
mv12-0≥0
解得μ≤
;
(3)小物块运动速度最大时,电场力与摩擦力的合力为零,设该位置离A点的距离为lA
则:
-
-μmg=0
解得lA=3L,即小物块运动到x=0时速度最大.
小物块从x=-2L运动到x=0的过程中,由动能定理得:
qU2-μmgs2=
mvm2-0
代入数据:q(φ0-
φ0)-μmg(2L)=
mvm2-0
解得vm=
(4)物块在AB之间运动大致的速度-时间关系图象可能为:
答:(1)固定在A处的电荷的电量QA为4Q.
(2)为了使小物块能够到达x=2L处,小物块与水平面间的动摩擦因数μ所满足的条件为μ≤
.
(3)若小物块与水平面间的动摩擦因数μ=
,小物块运动到离A点的距离为3L处时速度最大.最大速度vm为
.
(4)画出μ取值不同的情况下,物块在AB之间运动大致的速度-时间关系图象,如上图所示.
即合场强E合=0
所以
| kQA |
| rA2 |
| kQB |
| rB2 |
得
| kQA |
| (4L)2 |
| kQB |
| (2L)2 |
解得QA=4Q;
(2)物块先做加速运动再做减速运动,到达x=2L处速度vt≥0
从x=-2L到x=2L过程中,由动能定理得:
qU1-μmgs1=
| 1 |
| 2 |
即q(φ0-
| 3 |
| 7 |
| 1 |
| 2 |
解得μ≤
| qφ0 |
| 7mgL |
(3)小物块运动速度最大时,电场力与摩擦力的合力为零,设该位置离A点的距离为lA
则:
| k?q(4Q) |
| lA2 |
| k?qQ |
| (6L-lA)2 |
解得lA=3L,即小物块运动到x=0时速度最大.
小物块从x=-2L运动到x=0的过程中,由动能定理得:
qU2-μmgs2=
| 1 |
| 2 |
代入数据:q(φ0-
| 25 |
| 63 |
| 1 |
| 2 |
解得vm=
|
(4)物块在AB之间运动大致的速度-时间关系图象可能为:

答:(1)固定在A处的电荷的电量QA为4Q.
(2)为了使小物块能够到达x=2L处,小物块与水平面间的动摩擦因数μ所满足的条件为μ≤
| qφ0 |
| 7mgL |
(3)若小物块与水平面间的动摩擦因数μ=
| kqQ |
| 3mgL2 |
|
(4)画出μ取值不同的情况下,物块在AB之间运动大致的速度-时间关系图象,如上图所示.

练习册系列答案
相关题目




 为无限大的不带电的金属平板,现将一个带电量为
为无限大的不带电的金属平板,现将一个带电量为 的点电荷置于板右侧,并使金属板接地:已知金属板与点电荷之间的空间电场分布于等量异种电荷之间的电场分布类似,取大地电势为零。图中
的点电荷置于板右侧,并使金属板接地:已知金属板与点电荷之间的空间电场分布于等量异种电荷之间的电场分布类似,取大地电势为零。图中 以电荷
以电荷
 点电势低于零电势
点电势低于零电势 和
和 点的场强相同
点的场强相同 点的场强大于
点的场强大于
