��Ŀ����
 һ�ʵ���x��ԭ����������������Լ��ٶ�a���٣�����t0ʱ���ٶȱ�Ϊv0�������Լ��ٶ�-a�˶������ٶȱ�Ϊ-
һ�ʵ���x��ԭ����������������Լ��ٶ�a���٣�����t0ʱ���ٶȱ�Ϊv0�������Լ��ٶ�-a�˶������ٶȱ�Ϊ-| v0 |
| 2 |
| v0 |
| 4 |
| v0 |
| 8 |
�������ٶ�-ʱ��ͼ���ٶȵ������ű�ʾ�ٶȵķ����ʵ���0-t0ʱ�������ȼ���ֱ���˶���ƽ���ٶȵ���
��������ѧ֪ʶ�õ�λ�ƵĹ��ɣ��������λ�ƣ�
| v0 |
| 2 |
����⣺
A����ͼ�����ʵ���ٶ��������Ա仯�������������Եı仯����A����
B���ʵ���0-t0ʱ�������ȼ���ֱ���˶���ƽ���ٶȵ���
����B����
C��D�ʵ���0-t0ʱ����λ��Ϊx1=
v0?2t0=v0t0����2t0-4t0ʱ����λ��Ϊx2=-
?
t0=-
����4t0-6t0ʱ����λ��Ϊx3=
?
?
=
�����ʵ��˶���������ԭ���������Ϊx=x1+x2+x3��=
��n����ʱ��x=v0t0����C����D��ȷ��
��ѡD
A����ͼ�����ʵ���ٶ��������Ա仯�������������Եı仯����A����
B���ʵ���0-t0ʱ�������ȼ���ֱ���˶���ƽ���ٶȵ���
| v0 |
| 2 |
C��D�ʵ���0-t0ʱ����λ��Ϊx1=
| 1 |
| 2 |
| 1 |
| 2 |
| v0 |
| 2 |
| v0t0 |
| 4 |
| 1 |
| 2 |
| v0 |
| 4 |
| t0 |
| 2 |
| v0t0 |
| 16 |
| v0t0 | ||
1-(
|
��ѡD
������������ѵ���������ѧ֪ʶ����ʵ�����λ�ƣ�ͨ�����ɷ��ܽ���ɣ�����������ѧ֪ʶ������������������

��ϰ��ϵ�д�
 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
�����Ŀ
 һ�ʵ���x��ԭ����������������Լ��ٶ�a���٣�����t0ʱ���ٶȱ�Ϊv0�������Լ��ٶ�-a�˶������ٶȱ�Ϊ-
һ�ʵ���x��ԭ����������������Լ��ٶ�a���٣�����t0ʱ���ٶȱ�Ϊv0�������Լ��ٶ�-a�˶������ٶȱ�Ϊ-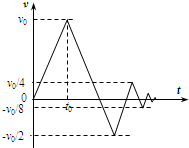 ��2009?�˲�ģ�⣩һ�ʵ���x��ԭ����������������Լ��ٶ�a���٣�����t0ʱ���ٶȱ�Ϊv0��������-a ���ٶ��˶������ٶȱ�Ϊ-
��2009?�˲�ģ�⣩һ�ʵ���x��ԭ����������������Լ��ٶ�a���٣�����t0ʱ���ٶȱ�Ϊv0��������-a ���ٶ��˶������ٶȱ�Ϊ- ʱ�����ٶ��ֱ�Ϊa��ֱ���ٶ�Ϊ
ʱ�����ٶ��ֱ�Ϊa��ֱ���ٶ�Ϊ ʱ�����ٶ��ٱ�Ϊ��a��ֱ���ٶȱ�Ϊ��
ʱ�����ٶ��ٱ�Ϊ��a��ֱ���ٶȱ�Ϊ�� ������v��tͼ����ͼ1��ʾ��������˵����ȷ����
(����)
������v��tͼ����ͼ1��ʾ��������˵����ȷ����
(����) 