题目内容
气球以4m/s的速度匀速竖直上升,气球下面挂一重物。在上升到12m高处系重物的绳子断了,从这时刻算起,重物落到地面的时间。
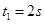
解析试题分析:挂重物的绳子断了以后,重物以4m/s的初速度做竖直上抛运动,规定向上的方向为正方向,对物体从绳子断到物体落地这段时间有: 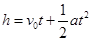 ,
,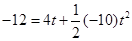
解得: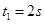
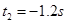 (舍去)
(舍去)
考点:考查了自由落体运动规律的应用

练习册系列答案
相关题目
关于自由落体运动,下列说法正确的是( )
| A.物体竖直向下的运动就是自由落体运动 |
| B.物体只在重力作用下从静止开始下落的运动叫自由落体运动 |
| C.初速度为零、加速度为g的匀变速直线运动就是自由落体运动 |
| D.当物体所受的空气阻力远小于本身重力时,物体从静止开始下落的运动可视为自由落体运动 |
关于自由落体运动,正确的说法是
| A.自由落体运动是一种匀变速运动 |
| B.自由落体的快慢与物体质量的大小有关 |
| C.在地球表面上各处,重力加速度大小相同 |
| D.物体只在重力作用下,在竖直方向上向下的运动就是自由落体运动 |
悬链长1.4m,从悬点处断开,使其自由下落,不计空气阻力,则整个悬链通过悬点下方3.2 m处的一点所需的时间为( )(取g=10m/s2)
| A.0.6s | B.0.8s | C.0.2s | D.1s |
如图所示是倾角为45°的斜坡,在斜坡底端P点正上方某一位置Q处以速度 水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为
水平向左抛出一个小球A,小球恰好能垂直落在斜坡上,运动时间为 .小球B从同一点Q处自由下落,下落至P点的时间为
.小球B从同一点Q处自由下落,下落至P点的时间为 .不计空气阻力,则
.不计空气阻力,则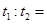 ( )
( )
| A.1∶2 | B. | C.1∶3 | D.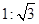 |
伽利略在研究自由落体运动性质的时候,为了排除物体自由下落的速度v随着下落高度h(位移大小)是均匀变化(即v=kh,k是个常数)的可能性,设计了如下的理想实验:在初速度为零的匀变速直线运动中,因为①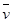 =
=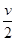 (式中
(式中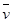 表示平均速度),而②h=
表示平均速度),而②h=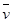 ·t,如果③v=kh成立的话,那么,必有h=
·t,如果③v=kh成立的话,那么,必有h= kht,即t=
kht,即t=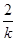 为常数.t竟然是与h无关的常数,这显然与常识相矛盾!于是,可以排除速度v是随着下落高度h均匀变化的可能性.关于伽利略这个理想实验中的逻辑及逻辑用语,你做出的评述是( )
为常数.t竟然是与h无关的常数,这显然与常识相矛盾!于是,可以排除速度v是随着下落高度h均匀变化的可能性.关于伽利略这个理想实验中的逻辑及逻辑用语,你做出的评述是( )
| A.全部正确 | B.①式错误 |
| C.②式错误 | D.③式以后的逻辑错误 |
一矿井深为125m,在井口每隔一定时间自由下落一小球。当第11个小球刚从井口开始下落时,第1个小球刚好到达井底,由此可知( )
| A.相邻小球开始下落的时间间隔为1.00s |
| B.相邻小球开始下落的时间间隔为0.50s |
| C.当第11个小球刚从井口开始下落时,第5个小球距井底45m |
| D.当第11个小球刚从井口开始下落时,第3个小球和第5个小球相距35m |
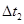 =0.4s,反应时间内视为匀速运动).已知甲车、乙车紧急刹车时产生的加速度大小分别为
=0.4s,反应时间内视为匀速运动).已知甲车、乙车紧急刹车时产生的加速度大小分别为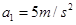 、
、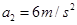 .
.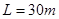 ,要避免闯红灯,他的反应时间
,要避免闯红灯,他的反应时间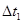 不能超过多少?
不能超过多少?