题目内容
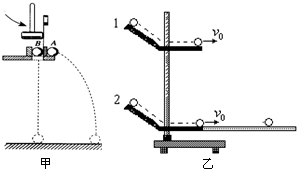
17. 某压力锅结构如图所示.盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起.假定在压力阀被顶起时,停止加热.
某压力锅结构如图所示.盖好密封锅盖,将压力阀套在出气孔上,给压力锅加热,当锅内气体压强达到一定值时,气体就把压力阀顶起.假定在压力阀被顶起时,停止加热.已知大气压强P随海拔高度H的变化满足P=P0(1-αH),其中常数α>0.结合气体定律定性分析在不同的海拔高度使用压力锅,当压力阀被顶起时锅内气体的温度有何不同.
分析 根据作用力的关系得出压强的关系,结合查理定律得出当压力阀被顶起时锅内气体的温度的变化.
解答 解:由P=P0(1-αH)(其中α>0)知,随着海拔高度的增加,大气压强减小.
由P1=P0+$\frac{mg}{S}$知,随着海拔高度的增加,阀门被顶起时锅内气体压强减小.
根据查理定律得:$\frac{P_1}{T_1}=\frac{P_2}{T_2}$
可知阀门被顶起时锅内气体温度随着海拔高度的增加而降低.
答:阀门被顶起时锅内气体温度随着海拔高度的增加而降低.
点评 该题结合高压锅的实际应用考查理想气体的状态方程,要注意理论联系实际,熟练应用查理定律定律即可正确解题.同时强调是热力学温标.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
5.关于重力的说法正确的是( )
| A. | 重力的方向是竖直向下的 | |
| B. | 同一个物体在地球上纬度不同的地方重力一定相同 | |
| C. | 重心一定是物体上最重的一点 | |
| D. | 重心一定是物体的几何中心 |
12.一质点做直线运动的v-t图象如图所示,则0-1s内和1s-3s内的速度和加速度相比较( )


| A. | 速度方向相反,加速度方向相反 | B. | 速度方向相同,加速度方向相反 | ||
| C. | 速度方向相反,加速度方向相同 | D. | 速度方向相同,加速度方向相同 |
5. 如图所示,已知带电小球A.B的电荷量分别为Q1,Q2,都用长为L的绝缘丝线悬挂在绝缘墙角0点处,静止时A,B相距为d为使重新平衡时A,B间距离减为$\frac{d}{2}$,可采用以下哪些方法( )
如图所示,已知带电小球A.B的电荷量分别为Q1,Q2,都用长为L的绝缘丝线悬挂在绝缘墙角0点处,静止时A,B相距为d为使重新平衡时A,B间距离减为$\frac{d}{2}$,可采用以下哪些方法( )
 如图所示,已知带电小球A.B的电荷量分别为Q1,Q2,都用长为L的绝缘丝线悬挂在绝缘墙角0点处,静止时A,B相距为d为使重新平衡时A,B间距离减为$\frac{d}{2}$,可采用以下哪些方法( )
如图所示,已知带电小球A.B的电荷量分别为Q1,Q2,都用长为L的绝缘丝线悬挂在绝缘墙角0点处,静止时A,B相距为d为使重新平衡时A,B间距离减为$\frac{d}{2}$,可采用以下哪些方法( )| A. | 将小球B的质量增加到原来的4倍 | |
| B. | 将小球B的质量增加到原来的8倍 | |
| C. | 将小球A,B的电荷量都减小到原来的一半 | |
| D. | 将小球A、B的电荷量都减小到原来的一半,同时将小球B的爬增加到原来的2倍 |
2.下列关于质点的说法正确的有( )
| A. | 正在做课间操的同学们都可以看做质点 | |
| B. | 研究打出的乒乓球旋转情况时可以把球看做质点 | |
| C. | 观察航空母舰上的舰载飞机起飞时,可以把航空母舰看做质点 | |
| D. | 在作战地图上确定航空母舰的准确位置时,可以把航空母舰看做质点 |
3.一质点做匀变速直线运动,初速度为2m/s,4s后速度大小变为10m/s,则质点的加速度大小可能为( )
| A. | 1m/s2 | B. | 2m/s2 | C. | 3m/s2 | D. | 4m/s2 |
 在如图所示的匀强电场中,长为L的绝缘细线一端系于O点,另一端系一带正电的小球,小球的电荷量$q=\frac{{\sqrt{3}mg}}{3E}$. 求:
在如图所示的匀强电场中,长为L的绝缘细线一端系于O点,另一端系一带正电的小球,小球的电荷量$q=\frac{{\sqrt{3}mg}}{3E}$. 求: 如图所示是一辆火车运动的位移-时间图象.线段OA和BC表示火车做什么运动?线段AB与横轴平行,表示火车做什么运动?火车在4min 内的位移是多少?通过12km用多长时间?火车在中途停了多长时间?
如图所示是一辆火车运动的位移-时间图象.线段OA和BC表示火车做什么运动?线段AB与横轴平行,表示火车做什么运动?火车在4min 内的位移是多少?通过12km用多长时间?火车在中途停了多长时间?