题目内容
17.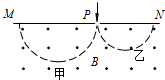 如图所示,甲、乙两个质量相同、带等量异种电荷的带电粒子,以不同的速率经小孔P垂直磁场边界MN,进入方向垂直纸面向外的匀强磁场中,在磁场中做匀速圆周运动,并垂直磁场边界MN射出磁场,半圆轨迹如图中虚线所示.不计重力空气阻力,则下列说法中正确的是( )
如图所示,甲、乙两个质量相同、带等量异种电荷的带电粒子,以不同的速率经小孔P垂直磁场边界MN,进入方向垂直纸面向外的匀强磁场中,在磁场中做匀速圆周运动,并垂直磁场边界MN射出磁场,半圆轨迹如图中虚线所示.不计重力空气阻力,则下列说法中正确的是( )| A. | 甲带负电荷,乙带正电荷 | |
| B. | 洛伦兹力对甲乙不做正功 | |
| C. | 甲的速率大于乙的速率 | |
| D. | 甲在磁场中运动的时间大于乙在磁场中运动的时间 |
分析 本题关键是明确粒子垂直射入匀强磁场后,在磁场中做匀速圆周运动,洛伦兹力提供向心力,根据牛顿第二定律列式分析轨道半径和公转周期,根据左手定则判断洛伦兹力方向
解答 解:A、在P点,速度向下,磁场向外,甲受向左的洛伦兹力,根据左手定则,甲带正电荷;
同理,在P点,乙受向右的洛伦兹力,速度向下,磁场向外,根据左手定则,乙带负电荷;故A错误;
B、根据左手定则,洛伦兹力与速度垂直,故洛伦兹力永不做功,故B错误;
C、粒子在磁场中做匀速圆周运动,根据牛顿第二定律,有:qvB=m$\frac{{v}^{2}}{R}$,故R=$\frac{mv}{qB}$,由于q、m、B均相同,甲的轨道半径大,说明甲的速度也大,故C正确;
D、周期T=$\frac{2πR}{v}$=$\frac{2πm}{qB}$,由于t=$\frac{1}{2}$T,故t=$\frac{πm}{qB}$;由于q、m、B均相同,故时间相等,故D错误;
故选:C.
点评 本题考查带电粒子在磁场中圆周运动的推论公式R=$\frac{mv}{qB}$,T=$\frac{2πR}{v}$=$\frac{2πm}{qB}$,的简单运用,同时要结合左手定则分析,基础题目.要注意负电荷受到的洛伦兹力的方向和正电荷受到的洛伦兹力的方向相反.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
7.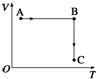 一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )
一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )
 一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )
一定质量的理想气体从状态A经状态B变化到状态C,这一过程在V-T图中表示如图所示,则下述结论错误的是( )| A. | 在过程AB中,气体压强不断变大 | B. | 在过程BC中,气体密度不断变大 | ||
| C. | 在过程AB中,气体对外界做功 | D. | 在过程BC中,外界对气体做功 |
8.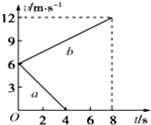 质量为0.5kg的物体在水平面上以一定的初速度运动,如图a、b分别表示物体不受拉力和受到水平拉力作用的v-t图象,则拉力与摩擦力大小之比为( )
质量为0.5kg的物体在水平面上以一定的初速度运动,如图a、b分别表示物体不受拉力和受到水平拉力作用的v-t图象,则拉力与摩擦力大小之比为( )
 质量为0.5kg的物体在水平面上以一定的初速度运动,如图a、b分别表示物体不受拉力和受到水平拉力作用的v-t图象,则拉力与摩擦力大小之比为( )
质量为0.5kg的物体在水平面上以一定的初速度运动,如图a、b分别表示物体不受拉力和受到水平拉力作用的v-t图象,则拉力与摩擦力大小之比为( )| A. | 1:2 | B. | 2:1 | C. | 3:1 | D. | 3:2 |
5.下列说法正确的是( )
| A. | 已知阿伏加德罗常数、气体摩尔质量和密度,可算出该气体分子间的平均距离 | |
| B. | 布朗运动是指悬浮在液体中的固体颗粒的无规则运动 | |
| C. | 给自行车轮胎打气时,打到后面很难打,是因为气体分子间存在斥力的缘固 | |
| D. | 物质是晶体还是非晶体,比较可靠的办法是从各向异性或各向同性来判断 | |
| E. | 热力学第二定律也叫做熵增加原理 |
2.某实验小组在进行光电效应实验中,发现用频率为ν的光照射光电管阴极时,发生了光电效应,下列操作的说法正确的是( )
| A. | 增大入射光的强度,光电流增大 | |
| B. | 减小入射光的强度,光电效应现象消失 | |
| C. | 改用频率小于ν的光照射,一定不发生光电效应 | |
| D. | 改用频率大于ν的光照射,光电子的最大初动能变大 | |
| E. | 此时如果加的是反向电压增大,则电流可能为零 |
9.下列说法正确的是( )
| A. | 自然界中进行的一切与热现象有关的宏观过程都具是可逆的 | |
| B. | 若气体的温度逐渐升高,其压强可以保持不变 | |
| C. | 温度相同的氢气和氧气,氢气分子和氧气分子的平均速率相同 | |
| D. | 只要知道气体的摩尔体积和阿伏加德罗常数,就可以算出气体分子的体积 |
6.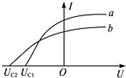 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )| A. | a光的频率更大 | |
| B. | 在增大电压U时,光电流一定都会增大 | |
| C. | 照射该光电管时a光单位时间发生的光电子数多 | |
| D. | 照射该光电管时b光使其逸出的光电子最大初动能大 |