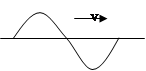题目内容
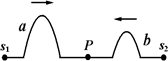
如图所示,一根张紧的水平弹性长绳上的a,b两点,相距14.0m,b点在a点的右方,当一列简谐横波沿此长绳向右传播时,若a点的位移达到正最大时,b点的位移恰为零且向下运动。经过1.00s后a点的位移为零,且向下运动,而b点的位移恰达到负最大,则这简谐波的波速可能等于


| A.4.67m/s | B.6m/s | C.10m/s | D.4m/s |
AC
【错解分析】错解:由对题目的分析可以知道,a,b之间间隔
 ,所以
,所以 =14.0m
=14.0m 
而
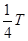 =1.00s T=4.00s
=1.00s T=4.00s由波速公式
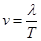 代入数据解得
代入数据解得v=4.67m/s选择A。
但此题可能多选,考虑到a,b之间满足条件的情况还可以为
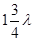 ,
,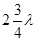 ……而第一状态与第二状态之间间隔时间为
……而第一状态与第二状态之间间隔时间为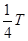 或1
或1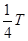
即当
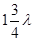 =14.0m,
=14.0m,
而1
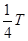 =1.00s,
=1.00s,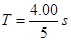
则波速
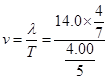
解得:v=10m/s 选择C
当
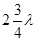 =14.0m,
=14.0m,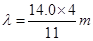
而2
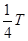 =1.00s,
=1.00s,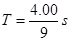
则波速
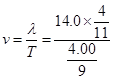
解得:v=11.5m/s显然不符合题目中的选项,且通过分析可知v=14m/s也是不对的,所以正确答案为A,C。
以上答案并没有错,但分析问题的过程出现了明显的错误,即把a,b之间存在
 ,
,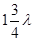 ,
,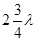 ……与两种状态之间的时间间隔
……与两种状态之间的时间间隔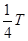 ,1
,1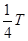 ,2
,2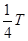 ……着两个没有必然联系的事件用意一一对应的关系联系起来,认为当a,b之间为
……着两个没有必然联系的事件用意一一对应的关系联系起来,认为当a,b之间为 时,必有间隔
时,必有间隔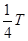 ,而a,b之间为1
,而a,b之间为1 时,必有间隔时间为1
时,必有间隔时间为1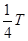 ……结果导致在计算过程中,漏了不少结论。而此题做为选择题,学生能用错误的思维方式得出符合答案的结果,纯属偶然。
……结果导致在计算过程中,漏了不少结论。而此题做为选择题,学生能用错误的思维方式得出符合答案的结果,纯属偶然。【正解】依题意,a,b之间为
 ,
,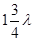 ,
,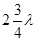 ……
…… +
+ ,或者为
,或者为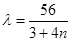 (n=0,1,2,3……)。而两个时刻之间的时间间隔为
(n=0,1,2,3……)。而两个时刻之间的时间间隔为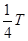 ,1
,1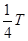 ,2
,2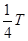 ……
……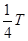 +NT
+NT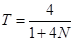 (N=0,1,2,3……)
(N=0,1,2,3……)波长λ有一系列数据,周期T也有一系列数据,从波的概念出发,两者并无一一对应,因而波速应为
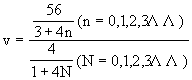
其解为当n=0,N=0,1,2……
n=1,N=0,1,2……
n=2,N=0,1,2……
我们可以通过列表来看一看波速的各种可能值:
| N | n | ||||
| 0 | 1 | 2 | 3 | … | |
| 0 | 4.67 | 2 | 1.27 | 0.933 | |
| 1 | 23.3 | 10 | 6.36 | 4.67 | |
| 2 | 42 | 18 | 11.5 | 8.4 | |
| 3 | 60.7 | 26 | 16.6 | 12.1 | |
| … | … | … | … | … | … |
【点评】这是1996年一道高考题,当年不少考生考试时也选对了答案,但这些考生思考问题时有着明显的片面性,只从n=N的情况去考虑问题,当n=N=0时,4.67m/s,当n=N=1时,v=10m/s,当n=N=2时v=11.5m/s……,把长度的周期性与时间的周期性混为一谈。若此题的四个选项中变化一个为v=2m/s(即n=1,N=0时),上述思维片面的考生可能就会漏选,因此,一定要对题目进行全面周到的分析。

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案
相关题目