题目内容
1.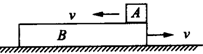 如图所示,质量为M=3.0kg的长方形木板B放在光滑水平地面上,在其右端放一质量为m=1.0kg的小木块A.现以地面为参考系,给A和B以大小均为4.0m/s,方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A并没有滑离木板,站在地面上的观察者看到一段时间内小木块A正在做加速运动,求这段时间内木板B相对地面的速度范围.
如图所示,质量为M=3.0kg的长方形木板B放在光滑水平地面上,在其右端放一质量为m=1.0kg的小木块A.现以地面为参考系,给A和B以大小均为4.0m/s,方向相反的初速度,使A开始向左运动,B开始向右运动,但最后A并没有滑离木板,站在地面上的观察者看到一段时间内小木块A正在做加速运动,求这段时间内木板B相对地面的速度范围.
分析 对A、B组成的系统,由动量守恒定律可以求出B的速度范围.
解答 解:A先向左做减速运动,后向右做加速运动,B一直向右做减速运动,当A的速度为0时,设B的速度为v1,以向右为正方向,由动量守恒定律得:
Mv0-mv0=Mv1
代入数据得:v1=$\frac{8}{3}=2.67$m/s
最后两者一起向右做匀速直线运动,设最终的速度为v,以向右为正方向,由动量守恒定律得:
Mv0-mv0=(M+m)v,
代入数据解得:v=2m/s;
这段时间内木板B相对地面的速度范围是:2m/s≤v≤2.67m/s
答:这段时间内木板B相对地面的速度范围是2m/s≤v≤2.67m/s.
点评 本题考查了求B的速度,分析清楚运动过程,应用动量守恒定律即可正确解题,分析清楚运动过程是正确解题的前提与关键.

练习册系列答案
相关题目
13.甲乙两人以相同的速度向西运动,则下列说法正确的是( )
| A. | 以甲为参照物,乙是运动的 | B. | 以地为参照物,甲是运动的 | ||
| C. | 以房子为参照物,甲是运动的 | D. | 以房子为参照物,甲是静止的 |
11.在下列图示的整个过程中,表示物体做匀变速直线运动的是( )
| A. | 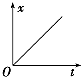 | B. | 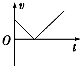 | C. | 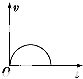 | D. | 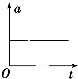 |


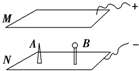 如图所示,金属板M接高压电源的正极,金属板N接负极.金属板N上有两个等高的金属柱A、B,其中A为尖头,B为圆头.逐渐升高电源电压,当电压达到一定值时,可看到放电现象.先产生放电现象的是A,这种放电现象叫做尖端放电.
如图所示,金属板M接高压电源的正极,金属板N接负极.金属板N上有两个等高的金属柱A、B,其中A为尖头,B为圆头.逐渐升高电源电压,当电压达到一定值时,可看到放电现象.先产生放电现象的是A,这种放电现象叫做尖端放电.