Question

【题目】如图所示是某游戏设施的简化图，由光滑圆弧轨道AB、半径R＝0.2 m的竖直圆轨道CDC、水平光滑轨道CE和粗糙水平轨道BC组成。NN'是一堵竖直墙，与E点的水平距离L＝4 m，MM'是一块长L0=2.4 m的软垫，水平轨道CE离地高度h＝3.2 m，M在E点的正下方。m＝1 kg的物体（可视为质点）从离水平轨道BC高H的圆弧轨道上的A点无初速度释放。已知物体与水平轨道BC间的动摩擦因数μ＝0.2，BC的长度x0＝9 m，重力加速度为g＝10 m／s2。

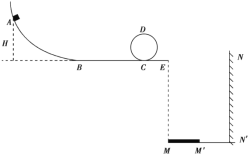
（1）若物体恰好能通过竖直圆轨道的最高点D，从E点水平抛出，求物体到达圆轨道最低点C时对轨道的压力；

（2）物体抛出后，若撞在竖直墙上，撞击前后，竖直方向上的速度大小、方向均不变，水平方向的速度大小不变，方向相反，欲使物体能顺利通过竖直圆轨道最高点且安全落在软垫MM'上，求物体释放高度H的取值范围。

Answer 1

【答案】（1）60 N，方向竖直向下；（2）4.25 m≤H≤6.8 m。

【解析】

(1)物体恰好能过最高点D有：

从C到D由机械能守恒得：

在C点有：

联立解得：

由牛顿第三定律可知，物体到达圆轨道最低点C时对轨道的压力大小为60N，方向竖直向下；

(2)由题意可知，要使物体能顺利通过竖直圆轨道最高点且安全落在软垫MM'上，物体从E飞出在水平方向的位移最大为2L（即打在M点），最小的位移为（L+L-L0）

物体运动的时间为：

从E点飞出的最大速度为：

最小速度为：

从A到E由动能定理得：

联立解得：4.25 m≤H≤6.8 m。