题目内容
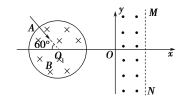
【题目】如图所示,直角坐标系xOy的y轴右侧有一宽为d的无限长磁场,磁感应强度大小未知,方向垂直纸面向外,y轴左侧有一个半径也为d的有界圆形磁场,磁感应强度为B,方向垂直纸面向里,圆心O1在x轴上,OO1=2d,一个带正电粒子以初速度v由A点沿AO1方向(与水平方向成60°角)射入圆形磁场并恰好从O点进入右侧磁场,从右边界MN上C点(没画出)穿出时与水平方向成30°角,不计粒子重力,求:
(1)粒子的比荷;
(2)右侧磁场的磁感应强度;
(3)粒子从A到C的运动时间。
【答案】(1) ![]() (2)
(2) ![]() B (3)
B (3) ![]()
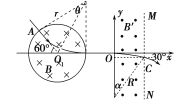
【解析】(1)粒子运动轨迹如图所示,粒子在磁场中由洛伦兹力提供向心力,在圆形磁场中有Bqv=m![]()
由图知r=dtan 60°=![]() d
d
联立得![]() =
=![]() 。
。
(2)在y轴右侧磁场中B′qv=m![]()
由图知R=2d
联立并代入比荷值得B′=![]() B。
B。
(3)粒子在圆形磁场中的运动时间t1=![]() ·
·![]() =
=![]()
粒子在两磁场间运动时间t2=![]()
粒子在y轴右侧磁场中运动时间t3=![]() ·
·![]() =
=![]()
所以粒子从A到C的运动时间为t=t1+t2+t3=![]() 。
。

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案
相关题目