题目内容
2008年9月27日,“神舟七号”宇宙飞船载着翟志刚等三名航天员进入了太空,中国航天员首次实现了在太空的舱外活动,这是我国航天发展史上的又一里程碑.已知万有引力常量为G,地球质量为M,地球半径为R.飞船绕地球做匀速圆周运动的过程中,距地面的高度为h,求:
(1)航天员在舱外活动时的加速度a的大小;
(2)飞船绕地球做匀速圆周运动的周期T.
(1)航天员在舱外活动时的加速度a的大小;
(2)飞船绕地球做匀速圆周运动的周期T.
分析:飞船绕地球做匀速圆周运动,地球对飞船的万有引力提供飞船的向心力,由万有引力定律和牛顿第二定律求解a和周期T.
解答:解:(1)航天员所受合力就是万有引力
应有:G
=ma
解得:a=
(2)飞船做圆周运动的向心力由万有引力提供
应有:G
=m
(R+h)
解得:T=2π(R+h)
答:(1)航天员在舱外活动时的加速度a的大小为
;
(2)飞船绕地球做匀速圆周运动的周期T为2π(R+h)
.
应有:G
| Mm |
| (R+h)2 |
解得:a=
| GM |
| (R+h)2 |
(2)飞船做圆周运动的向心力由万有引力提供
应有:G
| Mm |
| (R+h)2 |
| 4π2 |
| T2 |
解得:T=2π(R+h)
|
答:(1)航天员在舱外活动时的加速度a的大小为
| GM |
| (R+h)2 |
(2)飞船绕地球做匀速圆周运动的周期T为2π(R+h)
|
点评:解决飞船、人造地球卫星类型的问题常常建立这样的模型:卫星绕地球做匀速圆周运动,地球对卫星的万有引力提供卫星所需要的向心力.常常是万有引力定律与圆周运动知识的综合应用.

练习册系列答案
相关题目
 14①(供选用《选修1-1》物理课教材的学生做)
14①(供选用《选修1-1》物理课教材的学生做) 2008年9月27日,“神舟七号”航天员翟志刚首次实现了中国航天员在太空的舱外活动,这是我国航天发展史上的又一里程碑.已知引力常量为G,地球质量为M,地球半径为R.飞船绕地球做匀速圆周运动的过程中,距地面的高度为h,则飞船加速度a的大小为( )
2008年9月27日,“神舟七号”航天员翟志刚首次实现了中国航天员在太空的舱外活动,这是我国航天发展史上的又一里程碑.已知引力常量为G,地球质量为M,地球半径为R.飞船绕地球做匀速圆周运动的过程中,距地面的高度为h,则飞船加速度a的大小为( )
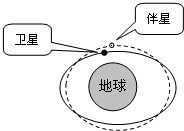 伴星是目前航天大国都在研究的一个新领域,我国于2008年9月27日成功释放了一颗“神七”轨道舱伴飞星.如图所示,为实现伴星的一种方案:卫星在图中实线椭圆轨道上运动,伴星的椭圆轨道(图中的虚线)长轴比卫星轨道长轴短一点(约几千米),而短轴比卫星轨道短轴大一点,两轨道共面,它们绕地球的运行周期基本相同.下列说法正确的是( )
伴星是目前航天大国都在研究的一个新领域,我国于2008年9月27日成功释放了一颗“神七”轨道舱伴飞星.如图所示,为实现伴星的一种方案:卫星在图中实线椭圆轨道上运动,伴星的椭圆轨道(图中的虚线)长轴比卫星轨道长轴短一点(约几千米),而短轴比卫星轨道短轴大一点,两轨道共面,它们绕地球的运行周期基本相同.下列说法正确的是( )