题目内容
19.如图所示,放在光滑水平面上的物体A和B,质量分别为M和m(M>m),水平恒力F作用在A上,A、B间的作用力为F1.水平恒力F作用在B上,A、B间的作用力为F2,则( )
| A. | $\frac{{F}_{1}}{{F}_{2}}$=$\frac{M}{m}$ | B. | F1=F2 | C. | F1+F2>F | D. | $\frac{{F}_{1}}{{F}_{2}}$=$\frac{m}{M}$ |
分析 对整体运用根据牛顿第二定律,研究加速度的关系.分别隔离B和A,由牛顿第二定律研究AB间作用力大小与F和两物体质量的关系.
解答 解:根据牛顿第二定律,对整体有:$a=\frac{F}{M+m}$;则两次物体运动的加速度大小相等.
第一次的情况下隔离B得:F1=ma,
第二次的情况下隔离A,得:F2=Ma,
则得:F1+F2=(M+m)a=F,
所以:F1:F2=m:M.故D正确,ABC错误;
故选:D.
点评 本题是连接体问题,要抓住加速度相同的特点,灵活选择研究对象.隔离时一般选择受力较少的物体研究内力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.根据电容器的定义式C=$\frac{Q}{U}$,可知( )
| A. | 电容器所带的电荷量Q越多,它的电容C就越大,C与Q成正比 | |
| B. | 电容器不带电,其电容即等于零 | |
| C. | 电容器两极板间的电压越高,它的电容就越小 | |
| D. | 电容器的电容大小与电容器带电荷量的多少无关 |
11.水中漩涡对游泳的人是很危险的,假如你恰处于漩涡的边缘,为尽快摆脱危险,你应该( )
| A. | 沿旋涡的切线逆漩流方向加速游 | B. | 沿旋涡的切线顺漩流方向加速游 | ||
| C. | 沿背离旋涡中心的方向加速游 | D. | 保持与漩涡中心相对静止 |
10. 如图所示,在竖直平面内有一矩形,其长边与一圆的底部相切于O点,现在有三条光滑轨道abc,它们的上端位于圆周上,下端在矩形的底边,三轨道都经过切点O,现在让一物块先后从三轨道顶端由静止下滑至底端,则物块在每一条倾斜轨道上滑动时所经历的时间关系为( )
如图所示,在竖直平面内有一矩形,其长边与一圆的底部相切于O点,现在有三条光滑轨道abc,它们的上端位于圆周上,下端在矩形的底边,三轨道都经过切点O,现在让一物块先后从三轨道顶端由静止下滑至底端,则物块在每一条倾斜轨道上滑动时所经历的时间关系为( )
 如图所示,在竖直平面内有一矩形,其长边与一圆的底部相切于O点,现在有三条光滑轨道abc,它们的上端位于圆周上,下端在矩形的底边,三轨道都经过切点O,现在让一物块先后从三轨道顶端由静止下滑至底端,则物块在每一条倾斜轨道上滑动时所经历的时间关系为( )
如图所示,在竖直平面内有一矩形,其长边与一圆的底部相切于O点,现在有三条光滑轨道abc,它们的上端位于圆周上,下端在矩形的底边,三轨道都经过切点O,现在让一物块先后从三轨道顶端由静止下滑至底端,则物块在每一条倾斜轨道上滑动时所经历的时间关系为( )| A. | ta<tb<tc | B. | ta>tb>tc | C. | ta=tb=tc | D. | 无法确定 |

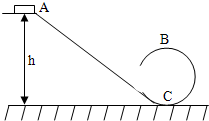 游乐场中的过山车从某一高度滑下后,进入竖直面上的圆轨道运动,当过山车经过圆轨道顶端时,也不会掉下来,是一种惊险刺激的运动,其简化模型如图所示,设此过山车质量为m,边山车自A点无初速沿轨道滑下后,进入圆轨道,圆轨道的半径为R,A点的高度h=5R,不计空气阻力和摩擦阻力.求过山车到圆轨道最高点B时的速度大小和对轨道的压力.
游乐场中的过山车从某一高度滑下后,进入竖直面上的圆轨道运动,当过山车经过圆轨道顶端时,也不会掉下来,是一种惊险刺激的运动,其简化模型如图所示,设此过山车质量为m,边山车自A点无初速沿轨道滑下后,进入圆轨道,圆轨道的半径为R,A点的高度h=5R,不计空气阻力和摩擦阻力.求过山车到圆轨道最高点B时的速度大小和对轨道的压力. 电量为+2×10-6C的带电体A放入电场中P点,受到电场力为4×10-4N方向竖直向下,求:
电量为+2×10-6C的带电体A放入电场中P点,受到电场力为4×10-4N方向竖直向下,求: