题目内容
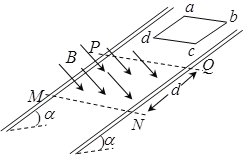
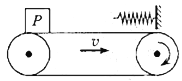
【题目】如图,水平传送带以恒定速度顺时针转动,传送带右端上方的挡板上固定着一轻弹簧。将小物块P轻放在传送带左端,P在接触弹簧前速度已达到v,与弹簧接触后弹簧的最大形变量为d。P的质量为m,与传送带之间的动摩擦因数为μ,最大静摩擦力等于滑动摩擦力,重力加速度为g。从P开始接触弹簧到弹簧第一次达到最大形变的过程中
A. P的速度一直减小
B. 传送带对P做功的功率一直减小
C. 传送带对P做的功W<μmgd
D. 弹簧的弹性势能变化量△Ek=![]() mv2+μmgd
mv2+μmgd
【答案】C
【解析】
A项:P与弹簧接触后在水平方向受弹簧力作用, P受的静摩擦力向右,P做匀速运动,运动到弹力与最大摩擦力相等时,P物体由惯性P继续压缩弹簧,P接下来做减速运动直到速度为零,故A错误;
B项:由公式![]() 可知,由于P先做匀速后做减速,由于静摩擦力增大,速度不变,所以功率先增大,后滑动摩擦力不变,速度减小,所以功率减小,故B错误;
可知,由于P先做匀速后做减速,由于静摩擦力增大,速度不变,所以功率先增大,后滑动摩擦力不变,速度减小,所以功率减小,故B错误;
C项:由于P开始到弹力与最大静摩擦力相等的过程中P受的为静摩擦力,后来为滑动摩擦力,所以传送带对P做的功小于μmgd,故C正确;
D项:对滑块由动能定理得:![]() ,由于
,由于![]() ,所以弹簧的弹性势能变化量小于
,所以弹簧的弹性势能变化量小于![]() mv2+μmgd,故D错误。
mv2+μmgd,故D错误。
故选:C。

练习册系列答案
相关题目