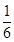题目内容
质量为m的物块在平行于斜面的力F作用下,从固定斜面的底端A由静止开始沿斜面上滑,经B点时速率为v,此时撤去F,物块滑回斜面底端时速率也为v,斜面倾角为θ,A、B间距离为x,则( )
A.整个过程中重力做功为
B.整个过程中物块克服摩擦力做功为 ;
;
C.上滑过程中克服重力做功为
D.从撤去F到物块滑回斜面底端,摩擦力做功为
D
解析试题分析:整个过程中,物体的初末位置重合,重力做功为零.故A错误;整个过程中,设物块克服摩擦力做功为Wf,根据动能定理得:Fx-Wf=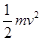 得Wf=Fx-
得Wf=Fx-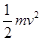 ,故B错误;上滑过程中物体克服重力做功为WG =mgxsinθ.或者上滑过程中由动能定理,Fx-WG-Wf=
,故B错误;上滑过程中物体克服重力做功为WG =mgxsinθ.或者上滑过程中由动能定理,Fx-WG-Wf=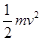 得 WG= Fx-Wf-
得 WG= Fx-Wf-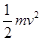 得故C错误.从撤去F到物块滑回斜面底端,设摩擦力做功为Wf′。
得故C错误.从撤去F到物块滑回斜面底端,设摩擦力做功为Wf′。
根据动能定理得:mgxsinθ+Wf′=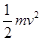 -
-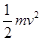 =0解得,Wf′=-mgxsinθ.故D正确.
=0解得,Wf′=-mgxsinθ.故D正确.
考点:动能定理的应用.

在静电场中将一个带电量为 的点电荷由a点移动到b点,已知a、b两点间的电势差
的点电荷由a点移动到b点,已知a、b两点间的电势差 。在此过程中,除电场力外,其他力做的功为
。在此过程中,除电场力外,其他力做的功为 ,则该点电荷的动能
,则该点电荷的动能
A.增加了 | B.减少了 |
C.增加了 | D.减少了 |
从地面竖直上抛一个质量为m的小球,小球上升的最大高度为H,设上升过程中空气阻力Ff恒定。在小球从抛出到上升至最高处的过程中,下列说法正确的是( )
| A.小球的机械能减少(mg+Ff)H | B.小球的动能减少mgH |
| C.小球的动能减少FfH | D.小球的机械能减少FfH |
如图所示,一竖直绝缘轻弹簧的下端固定在地面上,上端连接一带正电小球P,小球所处的空间存在着方向竖直向上的匀强电场,小球平衡时,弹簧恰好处于原长状态。现给小球一竖直向上的初速度,小球最高能运动到M点。在小球从开始运动到运动至最高点时,下列说法正确的是( )
| A.小球电势能的减少量大于小球重力势能的增加量 |
| B.小球机械能的改变量等于电场力做的功 |
| C.弹簧弹性势能的增加量等于小球动能的减少量 |
| D.小球动能的减少量等于电场力和重力做功的代数和 |
如图所示,粗糙程度均匀的绝缘斜面下方O点处有一正点电荷,带负电的小物体以初速度v1从M点沿斜面上滑,到达N点时速度为零,然后下滑回到M点,此时速度为v2(v2<v1).若小物体电荷量保持不变,OM=ON,则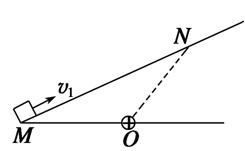
A.小物体上升的最大高度为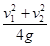 |
| B.从N到M的过程中,小物体的电势能逐渐减小 |
| C.从M到N的过程中,电场力对小物体先做负功后做正功 |
| D.从N到M的过程中,小物体受到的摩擦力和电场力均是先增大后减小 |
如图所示P和Q为两平行金属板,PQ两极板间电压为U,保持不变。在P板附近有一电子(重力不计)由静止开始向Q板运动,关于电子到达Q板时的速率,下列说法正确的是:( )
| A.两板间距离越大,加速时间越长,获得的速率就越大 |
| B.两板间距离越小,加速度越大,获得的速率就越大 |
| C.与两板间距离无关,仅与加速电压U有关 |
| D.以上说法都不正确 |
如图所示,a.b.c.d为匀强电场中的四个等势面,一个电子射入电场后的运动轨迹如实线MN所示,由此可知( )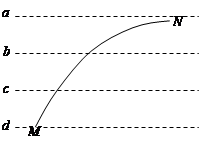
| A.电子在N的动能大于在M的动能 |
| B.电子在N的电势能小于在M的电势能 |
| C.电场强度方向向左 |
| D.电场中,a点电势低于b点电势 |
一水平放置的平行板电容器的两极扳间距为d,极扳分别与电池两极相连.上极板中心有一小孔(小孔对电场的影响可忽略不计)。小孔正上方d/2处的P点有一带电粒子,该粒子从静止开始下落.经过小孔进入电容器,并在下极板处未与极扳接触、返回。若将下极板向上平移d/3,则从P点开始下落的相同粒子将( )
| A.打到下极扳上 |
| B.在下极板处返回 |
| C.在距上极板d/2处返回 |
| D.在距上极扳2d/5处返回 |
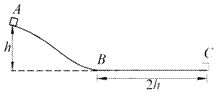
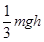 ;木块通过 B 点后继续滑行2h 距离后,在 C 点停下来,则木块与曲面间的动摩擦因数应为
;木块通过 B 点后继续滑行2h 距离后,在 C 点停下来,则木块与曲面间的动摩擦因数应为