题目内容
长L=0.5m的轻杆，其一端连接着一个零件A，A的质量m=2kg．现让A在竖直平面内绕O点做匀速圆周运动，如图所示．在A通过最高点时，求下列两种情况下A对杆的作用力．（g=10m/s2）：
（1）A的速率为1m/s；
（2）A的速率为4m/s．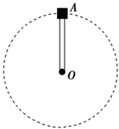
（1）A的速率为1m/s；
（2）A的速率为4m/s．
以A为研究对象，设其受到杆的拉力为F，则有
mg+F=m
．
（1）代入数据v=1 m/s，可得
F=m（
-g）=2×（
-10）N=-16 N，
即A受到杆的支持力为16 N．根据牛顿第三定律可得A对杆的作用力为压力16 N．
（2）代入数据v=4 m/s，可得
F=m（
-g）=2×（
-10）N=44 N，
即A受到杆的拉力为44 N．根据牛顿第三定律可得A对杆的作用力为拉力44 N．
答：（1）A的速率为1m/s，A对杆的作用力为压力16 N．
（2）A的速率为4m/s，A对杆的作用力为拉力44 N．
mg+F=m
| v2 |
| L |
（1）代入数据v=1 m/s，可得
F=m（
| v2 |
| L |
| 12 |
| 0.5 |
即A受到杆的支持力为16 N．根据牛顿第三定律可得A对杆的作用力为压力16 N．
（2）代入数据v=4 m/s，可得
F=m（
| v2 |
| L |
| 42 |
| 0.5 |
即A受到杆的拉力为44 N．根据牛顿第三定律可得A对杆的作用力为拉力44 N．
答：（1）A的速率为1m/s，A对杆的作用力为压力16 N．
（2）A的速率为4m/s，A对杆的作用力为拉力44 N．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
长L=0.5m的轻杆，其一端连接着一个零件A，A的质量m=2kg．现让A在竖直平面内绕O点做匀速圆周运动，如图所示．在A通过最高点时，求下列两种情况下A对杆的作用力．（g=10m/s2）：
如图所示，长L=0.5m的轻杆，其下端固定于O点，上端固定有质量m=2kg的小球，它绕O点在竖直平面内做匀速圆周运动，求下列情况下，小球通过最高点时杆对小球的力．（g=10m/s2）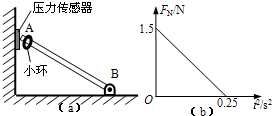
（2012?卢湾区一模）如图（a）所示，长L=0.5m的轻杆AB，一端通过铰链固定于地面，另一端靠在固定于竖直墙壁上的压力传感器上．现将一质量m=0.2kg的小环套在轻杆上，t=0时刻从A处由静止释放小环，压力传感器的示数FN随时间平方变化的FN-t2图象如图（b）所示． 则在小环下滑过程的中间时刻，压力传感器承受的压力大小为
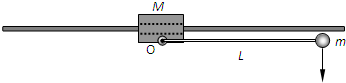如图所示，质量M=2kg的滑块套在光滑的水平轨道上，质量m=1kg的小球（视为质点）通过长L=0.5m的轻杆与滑块上的光滑轴O连接，滑块和轨道不会影响到小球和轻杆在竖直平面内绕O轴的转动．开始时轻杆处于水平状态．现给小球一个竖直向下的初速度，取g=10m/s2．