题目内容
11.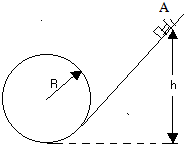 两辆相同的小车(大小可忽略不计),中间夹住被压缩的轻弹簧后用细线捆绑在一起,从光滑斜轨上某处A一起由静止滑下.斜轨末端紧接一个半径为R的光滑圆环,当两车刚滑到圆环最低点时,细线突然断开,弹簧将两车迅速弹开,其中后一辆车停在原处,前一辆车沿圆环运动恰好能通过最高点.求:
两辆相同的小车(大小可忽略不计),中间夹住被压缩的轻弹簧后用细线捆绑在一起,从光滑斜轨上某处A一起由静止滑下.斜轨末端紧接一个半径为R的光滑圆环,当两车刚滑到圆环最低点时,细线突然断开,弹簧将两车迅速弹开,其中后一辆车停在原处,前一辆车沿圆环运动恰好能通过最高点.求:(1)前一辆车被弹出时的速度;
(2)把车弹出时弹簧释放的弹性势能;
(3)斜轨上A处到轨道最低点的高度h.
分析 (1)前车沿圆环轨道运动恰能越过圆弧轨道最高点,根据牛顿第二定律求出最高点速度,根据机械能守恒列出等式求解;
(2)由动量守恒定律求出两车分离前速度,根据系统机械能守恒求解;
(3)两车从h高处运动到最低处,根据机械能守恒列出等式求解.
解答 解:(1)前车恰好能通过最高点,在最高点有:mg=$m\frac{{v}^{2}}{R}$…①
设前车被弹出时速度为v1,它在上滑过程中机械能守恒有:$\frac{1}{2}$mv12=$\frac{1}{2}$mv2+mg•2R…②,
由①②解得:v1=$\sqrt{5gR}$
(2)设线断前两车速度为v0,根据动量守恒,有:2mv0=mv1…③
弹簧释放的弹性势能为:
EP=$\frac{1}{2}$mv12-$\frac{1}{2}$•2mv02=1.25 mgR …④
(3)两车下滑过程中机械能守恒有:
2mgh=$\frac{1}{2}$•2mv02 …⑤
解得:h=$\frac{5}{8}$R
答:(1)前一辆车被弹出时的速度为$\sqrt{5gR}$;
(2)把车弹出时弹簧释放的弹性势能为1.25 mgR;
(3)斜轨上A处到轨道最低点的高度h为$\frac{5}{8}$R.
点评 本题综合性较强,解决综合问题的重点在于分析物体的运动过程,分过程灵活应用相应的物理规律;优先考虑动能定理、机械能守恒等注重整体过程的物理规律.

练习册系列答案
相关题目
4. 如图所示,轻弹簧的一端与物块P相连,另一端固定在木板上.先将木板水平放置,并使弹簧处于拉伸状态.缓慢抬起木板的右端,使倾角逐渐增大,直至物块P刚要沿木板向下滑动,在这个过程中,正确的说法是( )
如图所示,轻弹簧的一端与物块P相连,另一端固定在木板上.先将木板水平放置,并使弹簧处于拉伸状态.缓慢抬起木板的右端,使倾角逐渐增大,直至物块P刚要沿木板向下滑动,在这个过程中,正确的说法是( )
 如图所示,轻弹簧的一端与物块P相连,另一端固定在木板上.先将木板水平放置,并使弹簧处于拉伸状态.缓慢抬起木板的右端,使倾角逐渐增大,直至物块P刚要沿木板向下滑动,在这个过程中,正确的说法是( )
如图所示,轻弹簧的一端与物块P相连,另一端固定在木板上.先将木板水平放置,并使弹簧处于拉伸状态.缓慢抬起木板的右端,使倾角逐渐增大,直至物块P刚要沿木板向下滑动,在这个过程中,正确的说法是( )| A. | 物块p对木板的压力逐渐增大 | |
| B. | 物块P所受静摩擦力的大小是先减小后增大 | |
| C. | 物块p所受静摩擦力的大小是先增大后减小 | |
| D. | 物块p所受重力沿斜面向下分力与摩擦力的合力大小始终不变 |
6. 汽车从车站出发行驶500s,速度达到20m/s.其运动v-t图线如图所示,则在这段时间里汽车行驶的距离不可能是( )
汽车从车站出发行驶500s,速度达到20m/s.其运动v-t图线如图所示,则在这段时间里汽车行驶的距离不可能是( )
 汽车从车站出发行驶500s,速度达到20m/s.其运动v-t图线如图所示,则在这段时间里汽车行驶的距离不可能是( )
汽车从车站出发行驶500s,速度达到20m/s.其运动v-t图线如图所示,则在这段时间里汽车行驶的距离不可能是( )| A. | 10km | B. | 8km | C. | 2km | D. | 4km |
1.关于物理学家和他们的贡献,下列说法中正确的是( )
| A. | 奥斯特发现了电流的磁效应 | |
| B. | 库仑提出了库仑定律,并最早实验测得元电荷e的数值 | |
| C. | 开普勒发现了行星运动的规律,并通过实验测出了万有引力常量 | |
| D. | 牛顿不仅发现了万有引力定律,而且提出了场的概念 |
 2010年温哥华冬奥会上,瑞典女队获得冰壶比赛世界冠军.假设冰壶在水平冰面上的一次滑行可简化为如下过程:如图所示,运动员将静止于O点的冰壶(视为质点)沿直线OO′推到A点放手,此后冰壶沿AO′滑行,最后停于C点.已知冰面与冰壶间的动摩擦因数为μ,冰壶质量为m,AC=L,CO′=r,重力加速度为g.
2010年温哥华冬奥会上,瑞典女队获得冰壶比赛世界冠军.假设冰壶在水平冰面上的一次滑行可简化为如下过程:如图所示,运动员将静止于O点的冰壶(视为质点)沿直线OO′推到A点放手,此后冰壶沿AO′滑行,最后停于C点.已知冰面与冰壶间的动摩擦因数为μ,冰壶质量为m,AC=L,CO′=r,重力加速度为g. 如图所示,在光滑的水平面上钉两个钉子A和B,A、B相距d=20cm,用一根长l=1m的细绳,一端系质量为m=0.4kg的小球,另一端固定在钉子A上,开始时球与钉子A、B在同一直线上,然后使小球以v=2m/s的速度开始在水平面内做匀速圆周运动,若绳子能承受的拉力为4N时恰好断裂,求:
如图所示,在光滑的水平面上钉两个钉子A和B,A、B相距d=20cm,用一根长l=1m的细绳,一端系质量为m=0.4kg的小球,另一端固定在钉子A上,开始时球与钉子A、B在同一直线上,然后使小球以v=2m/s的速度开始在水平面内做匀速圆周运动,若绳子能承受的拉力为4N时恰好断裂,求: 如图所示是一匀强电场,已知场强E=2×102 N/C,现让一个带电荷量q=-4×10-8 C的电荷沿电场方向从M点移到N点,M、N间的距离x=30cm.试求:
如图所示是一匀强电场,已知场强E=2×102 N/C,现让一个带电荷量q=-4×10-8 C的电荷沿电场方向从M点移到N点,M、N间的距离x=30cm.试求: